Angular velocity  (Page 4/4)

In case, these instantaneous axes are parallel to each other, then it is possible to assign unique angular velocity of the particle about any one of these instantaneous axes. We shall work out an example here to illustrate determining angular velocity about an instantaneous axis.

Example 3

Problem 3 : A rod of length 10 m lying against a vertical wall starts moving. At an instant, the rod makes an angle of 30° as shown in the figure. If the velocity of end “A” at that instant, is 10 m/s, then find the angular velocity of the rod about “A”.

Motion of a rod

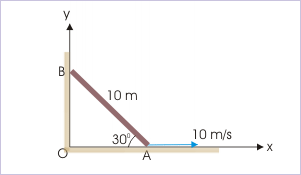
Solution : In this case, the point about which angular velocity is to be determined is itself moving towards right with a velocity of 10 m/s. However, the instantaneous axis of rotation is parallel to each other. As such, it is possible to assign unique angular velocity for the motion under consideration.

We shall examine the situation with the geometric relation of the length of rod with respect to the position of its end “A”. This is a logical approach as the relation for the position of end “A” shall let us determine both linear and angular velocity.

Motion of a rod

$$\begin{array}{l}x=\mathrm{AB}\cos \theta \end{array}$$

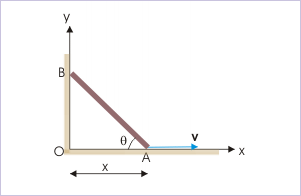
Note here that length of rod is constant. An inspection of the equation reveals that if we differentiate the equation with respect to time, then we shall be able to relate linear velocity with angular velocity.

$$\begin{array}{l}\frac{đx}{đt}=\mathrm{AB}\frac{đ}{đt}\left(\cos \theta \right)=-\mathrm{AB}\sin \theta x\frac{đ\theta }{đt}\end{array}$$

$$\begin{array}{l}\Rightarrow v=-\mathrm{AB}\omega \sin \theta \\ \Rightarrow \omega =-\frac{v}{\mathrm{AB}\sin \theta }\end{array}$$

Putting values,

$$\begin{array}{l}\Rightarrow \omega =-\frac{10}{10\sin 30°}=-2\mathrm{rad}/s\end{array}$$

Negative sign here needs some clarification. We can visualize that rod is rotating about instantaneous axis in anticlockwise direction. As such, the sign of angular velocity should have been positive - not negative. But, note that we are measuring angle from the negative x-direction as against positive x-direction. Therefore, we conclude that the negative sign in this instant case represents rotation of rod about the instantaneous axis in anticlockwise direction.

Motion of a rod

Summary

1: Angular quantities are general quantities, which can be defined and interpreted for any motion types – pure/impure translation or rotation.

2: Angular velocity is defined as the time rate of change of angular displacement with respect to a point :

$$\begin{array}{l}\mathbf{\omega }=\frac{d\mathbf{\theta }}{d\mathbf{t}}\end{array}$$

3: If the point, about which angular velocity is determined, is the origin of the reference system, then the position of the particle is represented by position vector.

4: The measurement and physical interpretation of angular velocity are different than that in the case of circular (rotational) motion about an axis.

5: The relation between linear and angular velocity has the following form,

$$\begin{array}{l}\mathbf{v}=\mathbf{\omega }\mathbf{x}\mathbf{r}\end{array}$$

where “ r ” determines the position of the particle with respect to the point. The magnitude of angular velocity can be determined, using any of the following two relations :

$$\begin{array}{l}\omega =\frac{v\sin \theta }{r}\end{array}$$

and

$$\begin{array}{l}\omega =\frac{v_{\perp }}{r}\end{array}$$

where " $v_{\perp }$ " denotes tangential component of the velocity vector, which is perpendicular to the position vector.

7: Direction of angular velocity is perpendicular to the plane of motion. The plane of motion, however, may not be fixed like in the case of rotation. We define plane of motion, which contains origin (or point) and tangential component of velocity.