2.3 Accelerated motion in one dimension  (Page 2/3)

Acceleration – time plot

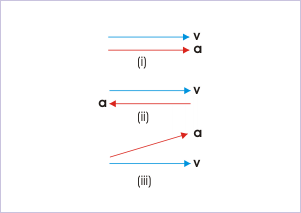
The requirement of one dimensional motion characterizes the nature of acceleration involved. The acceleration may vary in magnitude only. No sideway directional change in acceleration of the motion is possible for a given external force. We must emphasize that there may be reversal of motion i.e. velocity even without any directional change in acceleration. A projectile, thrown up in vertical direction, for example, returns to ground with motion reversed at the maximum height, but acceleration at all time during the motion is directed downwards and there is no change in the direction of acceleration.

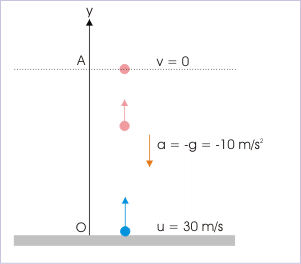
Motion under gravity

In mathematical parlance, if v = A i , then a = B i , where A and B are positive or negative numbers. For one dimensional motion, no other combination of unit vectors is possible. For example, acceleration can not be a = B j or a = B( i + j ).

We summarize the discussion as :

• The velocity and force (hence acceleration) are directed along a straight line.
• For a given external force, the direction of acceleration remains unchanged in one dimension.

Graphs of one dimensional motion

Graphs are signature of motion. Here, we shall discuss broad categories of motion types in terms of acceleration and velocity.

Acceleration – time plot

Acceleration can be zero, constant or varying, depending upon the net external force and mass of the body. It is imperative that a single motion such as the motion of a car on the road may involve all kinds of variations in acceleration. A representation of an arbitrary real time acceleration - time variation may look like :

Acceleration – time plot

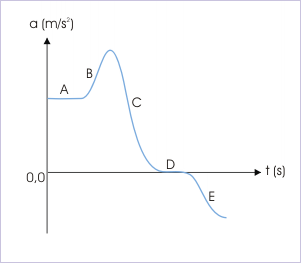
We can interpret this plot if we know the direction of velocity. We consider that positive direction of velocity is same as that of acceleration. Section, A, in the figure, represents constant acceleration. Section B represents an increasing magnitude of acceleration, whereas section C represents a decreasing magnitude of acceleration. Nonetheless, all of these accelerations result in the increase of speed with time as both velocity and acceleration are positive (hence in the same direction). The section E, however, represents deceleration as velocity (positive) and acceleration (negative) are in opposite direction. There is no acceleration during motion corresponding to section D. This section represents uniform motion.

$$\begin{array}{l}\text{For section A : Constant acceleration :}a=\frac{đv}{đt}=\text{Constant}\\ \text{For section B and C : Positive acceleration :}a=\frac{đv}{đt}>\text{0}\\ \text{For section D : Zero acceleration :}a=\frac{đv}{đt}=\text{0}\\ \text{For section E : Negative acceleration :}a=\frac{đv}{đt}<\text{0}\end{array}$$

Area under acceleration - time plot

We know that :

$$\begin{array}{l}a=\frac{đv}{đt}\\ \Rightarrow đv=ađt\end{array}$$

Integrating both sides, we have :

$$\begin{array}{l}\Delta v=a\Delta t\end{array}$$

Thus, areas under acceleration – time plot gives the change in velocity in a given interval.

Velocity – time plot

Here, we discuss velocity – time plot for various scenarios of motion in one dimension :

1: Acceleration is zero

If acceleration is zero, then velocity remains constant. As such the velocity time plot is a straight line parallel to time axis.