| << Chapter < Page | Chapter >> Page > |
The important thing to understand here is that speeds of the board and that of central axis of the cylinder are not same. The top of the cylinder moves at a speed “2v”, if the central axis of the cylinder moves at speed “v”. Now, the speed of the board is same as that of the top of the cylinder. Hence, if board moves by a distance “x”, the COM of the cylinder moves by “x/2”.
Pure rolling of a cylinder

The distance covered by the person is :
According to question,
and distance moved by the cylinder is :
Example 4
Problem : A disk of radius “R” rolls over a horizontal surface along a straight line with a constant velocity, “v”. If the point of contact with the surface at time t = 0 is the origin of the coordinate system, then determine the coordinates of the particle at the contact after time “t”.
Solution : In general, the center of mass of the disk transverses a linear distance, x, :
Let the particle makes an angle “θ” with the vertical after time “t” as shown in the figure. If “x” and “y” be the coordinates of its position in the coordinate system, then
Pure rolling motion
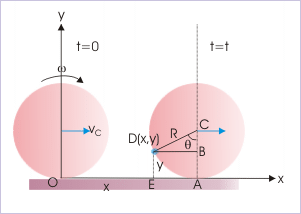
But, angular displacement “θ” is :
Hence, coordinates are :
Example 5
Problem : A disk of radius “R” rolls on a horizontal surface with a velocity “v”. Find the velocity of a particle at a point “P” (as shown in the figure).
Velocity of a particle in pure rolling motion

Solution : The velocity of point “P” is the vector sum of velocities due to (i) pure translation and (i) pure rotation.
For pure translation, each particle constituting the body moves with the same speed as that of its COM, which is “v” as given in the question. Thus, velocity due to translation is :
Velocity of a particle in pure rolling motion
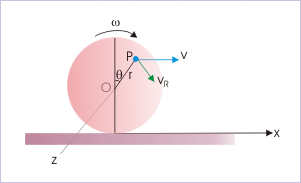
For pure rotation, each particle constituting the body moves with the same angular velocity, “ω“. The tangential linear speed of point “P” due to rotation is :
This velocity acts tangentially at the point “P” as shown in the figure. In component form, the linear velocity due to pure rotation is :
Velocity of a particle in pure rolling motion
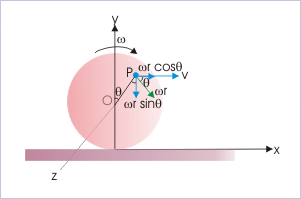
Combining velocities due to translation and rotation, we have :
For rolling motion, we know that angular velocity is related to velocity of COM as :
Substituting in the expression of velocity of the point “P”, we have :
This equation is the general equation for the velocity of a particle constituting the rigid body in pure rolling. For a particle on the rim of the disk (r = R), the relation reduces to :
It is interesting to evaluate this expression of the velocity for the particle on the rim for certain knows positions. This may be taken up as an exercise to calculate velocities at top most and at bottom most positions and to see whether results match with that determined earlier.

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?