| << Chapter < Page | Chapter >> Page > |
Mi of a cross about angle bisector
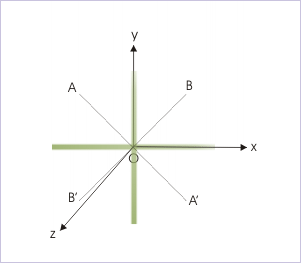
The MIs about the two bisectors are equal by the symmetry of the cross about them. Hence,
Thus,
Example 3
Problem : The MI of a solid sphere is calculated about an axis parallel to one of its diameter, at a distance "x" from the origin. The values are plotted against distance. Which of the four plots, as shown below, correctly describes the variation of MI with respect to "x" for the solid sphere.
Plots of mi .vs. distance
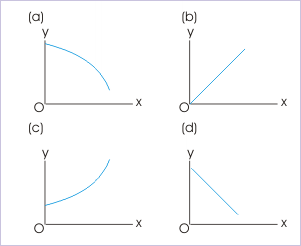
Solution : It is evident that farther the axis from the origin, greater is MI about that axis. We can, thus, conclude that the plot between MI and the distance should be increasing one with increasing distance ("x"). Thus, options (a) and (d) are incorrect. Now, the MI of solid sphere about an axis parallel to one of diameters, at a distance "x" from the origin is given as :
Plots of mi .vs. distance
where is MI about one of the diameters and is a constant for the given solid sphere. Thus, the equation above takes the form of the equation of parabola,
The correct plot, therefore, is an increasing parabola as shown in Figure (c).
Example 4
Problem : Four holes of radius "L/4" are made in a thin square plate of mass "M" and side "L" in "xy" - plane, as shown in the figure. Find its MI about z – axis.
Mi of remaining body
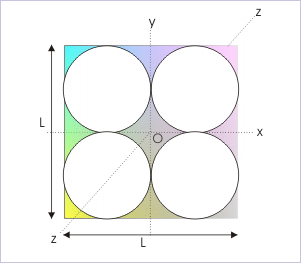
Solution : MI is a scalar quantity. It means that MI has no directional attribute. Thus, we can conclude that MI of the complete plate is equal to the sum of MIs of remaining plate and that of the four circular disks taken out from the plate about z-axis. Hence, MI of remaining plate is obtained as :
Now, according to theorem of perpendicular axes, the MI of complete square about z-axis is two times its MI about x-axis :
Further, according to theorem of parallel axes, the MI of circular disk of mass “m” and radius “L/4” about the same z-axis is :
Mi of remaining body
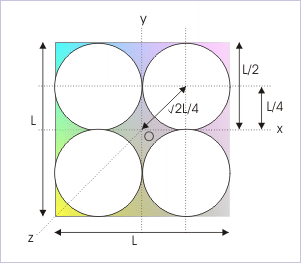
The mass of the disk "m" is given by multiplying areal density with the area of the circular disk,
Substituting for "m", we have :
Thus, the required MI is :
Example 5
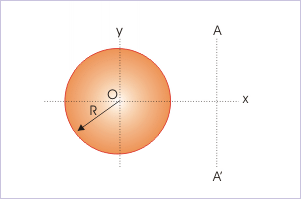
Problem : A thin wire of length "L" and uniform linear mass density "λ" is bent into a circular loop. Find the MI of the loop about an axis AA' as shown in the figure.
Mi of a circular loop
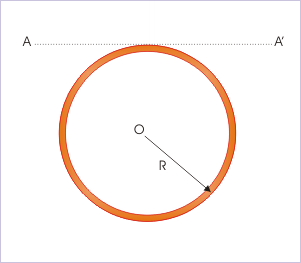
Solution : The MI of the circular loop about a tangential axis AA' is found out by the theorem of parallel axis :
Mi of a circular loop
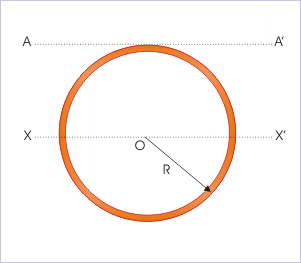
where IXX' is the MI about an axis which is one of the diameters of the ring and is parallel to tangential axis AA'. Now, MI about the diameter can be calculated applying theorem of perpendicular axes :
where is MI about an axis perpendicular to the surface of loop and passing through center of mass (ZZ' axis). It is given by the expression :
Mi of a circular loop
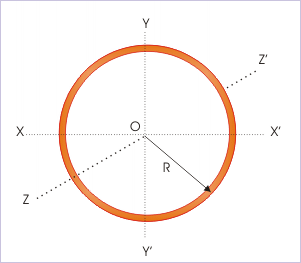
Combining two equations, we have :
Putting this in the expression of , we have :
Now, we are required to find mass and radius from the given data. Here,
Since the wire is bent into a circle, the perimeter of the circle is equal to the length of the wire. Hence,
Putting these values in the expression of MI about AA' axis is :
Example 6
Problem : A uniform wire of mass "M" and length "L" is bent into a regular hexagonal loop. Find its MI about an axis passing through center of mass and perpendicular to its surface.
Solution : We find MI of hexagonal loop in following three steps :
The MI of the side about perpendicular axis through center of mass of the side is :
Mi of a regular hexagonal loop

By the geometry of a side with respect to center, the traingle OPQ is a right angle triangle. We have perpendicular distance "R" between axes AA' and ZZ' as :
Mi of a side of regular hexagonal loop

Applying theorem of parallel axes, the MI about perpendicular axis through center of mass of the loop is :
Now, adding MIs of each side, the required MI about perpendicular axis through center of mass of the loop is :

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?