18.8 Theorems on moment of inertia  (Page 14/3)

The use of integral expression of moment of inertia (MI) for a rigid body can be employed to calculate MI about different axes of rotation. However, such consideration is tedious because of difficulty in integral evaluation. There are two theorems, which avoid integral evaluation for calculating MI about certain other axes, when moment of inertia about an axis is known. The theorems are (i) theorem of parallel axes and (ii) theorems of perpendicular axes.

Theorem of parallel axes

This theorem enables us to calculate MI about any axis, parallel to the axis passing through center of mass (COM). The mathematical expression of this theorem is given as :

where $I_C$ is MI of the body about an axis passing through center of mass, "C"; I is MI of the body about an axis parallel to the axis passing through center of mass; "M" is the mass of the rigid body and "d" is the perpendicular distance between two parallel axes.

We shall here drive expression for the MI about parallel axis in a general case of arbitrarily shaped three dimensional rigid body. This derivation requires clear visualization in three dimensional coordinate space. We shall use three figures to bring out relative distances and angles in order to achieve the clarity as stated.

Let "M" be the mass of the rigid body and "dm" be the mass of a small element. Let "C" be the center of mass and "Cz" be an axis of rotation as shown in the figure. For convenience, we consider that "Cz" is along z-coordinate of the reference system.

Theorem of parallel axes

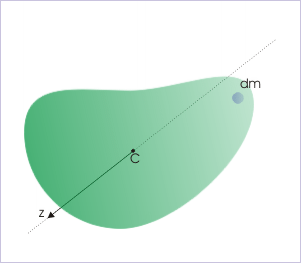
In general, the elemental mass "dm" may be situated anywhere in relation to the axis "cz". Here, we consider two cross sections of the rigid body in parallel planes, which are perpendicular to z - axis (axis of rotation). The two cross sections are drawn here such that one (on the rear) contains center of mass "C" and other (on the front) contains the elemental mass "dm". We designate the plane containing elemental mass "dm" as xy-plane of the coordinate system.

Theorem of parallel axes

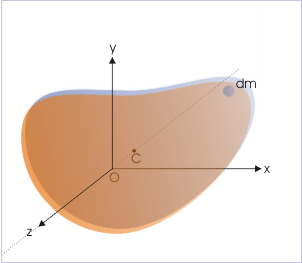
Now we concentrate on the plane (the plane in the front) containing elemental mass "dm". The element of mass "dm" being in the xy-plane has z = 0 and its position is given by two coordinates "x" and "y".

The parallel axis through center of mass intersects the plane (xy) at point "O". Let Az' be the parallel axis about which, we have to calculate MI of the rigid body. This axis intersects the plane (xy) at point "A" as shown in the figure below.

In order to comprehend three dimensional aspect of perpendicular lines, we should realize that all lines drawn on the plane (xy) are perpendicular to two parallel axes (Oz or Az') as xy plane is perpendicular to them. The line BA in the xy plane, therefore, represents the perpendicular distance of elemental mass "dm" from the axis Az'. Similarly, the line BO represents the perpendicular distance of elemental mass "dm" from the axis Oz. Also, the line OA in xy-plane is perpendicular distance between two parallel axes, which is equal to "d".