| << Chapter < Page | Chapter >> Page > |
The planar components of a vector lies in the plane of vector. Since there are two perpendicular axes involved with a plane, a vector is resolved in two components which lie in the same plane as that of vector. Clearly, a vector is composed of components in only two directions :
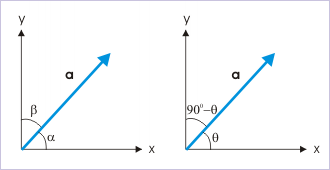
From the figure depicting a planar coordinate, it is clear that angle “β” is compliment of angle “α”. If α = θ, then
Planar vector
Putting in the expression for the vector,
From graphical representation, the tangent of the angle that vector makes with x-axis is :
Similarly, the tangent of the angle that vector makes with y-axis is :
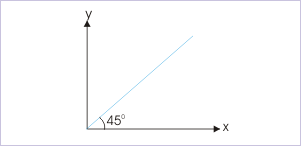
Problem : Find the unit vector in the direction of a bisector of the angle between a pair of coordinate axes.
Solution : The unit vector along the direction of a bisector lies in the plane formed by two coordinates. The bisector makes an angle of 45° with either of the axes. Hence, required unit vector is :
Unit vector
Note : We may check that the magnitude of the unit vector is indeed 1.
The angle involved in determination of components plays important role. There is a bit of ambiguity about angle being used. Actually, there are two ways to write a vector in component form. We shall illustrate these two methods with an illustration. Let us consider an example. Here, we consider a vector OA having magnitude of 10 units. The vector makes 150° and 30° angle with x and y axes as shown in the figure.
Component of a vector
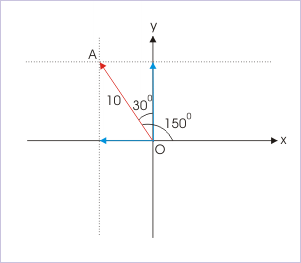
Using definition of components, the vector OA is represented as :
Note that we use angles that vector makes with the axes to determine scalar components. We obtain corresponding component vectors by multiplying scalar components with respective unit vectors of the axes involved. We can, however, use another method in which we only consider acute angle – irrespective of directions of axes involved. Here, vector OA makes acute angle of 60° with x-axis. While representing vector, we put a negative sign if the component is opposite to the positive directions of axes. We can easily determine this by observing projection of vector on the axes. Following this :
Note that we put a negative sign before component along x-direction as projection of vector on x-axis is in opposite direction with respect to positive direction of x-axis. The y - projection, however, is in the positive direction of y-axis. As such, we do not need to put a negative sign before the component. Generally, people prefer second method as trigonometric functions are positive in first quadrant. We are not worried about the sign of trigonometric function at all.

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?