| << Chapter < Page | Chapter >> Page > |
(a) At what angle will light traveling in air be completely polarized horizontally when reflected from water? (b) From glass?
Strategy
All we need to solve these problems are the indices of refraction. Air has water has and crown glass has . The equation can be directly applied to find in each case.
Solution for (a)
Putting the known quantities into the equation
gives
Solving for the angle yields
Solution for (b)
Similarly, for crown glass and air,
Thus,
Discussion
Light reflected at these angles could be completely blocked by a good polarizing filter held with its axis vertical . Brewster’s angle for water and air are similar to those for glass and air, so that sunglasses are equally effective for light reflected from either water or glass under similar circumstances. Light not reflected is refracted into these media. So at an incident angle equal to Brewster’s angle, the refracted light will be slightly polarized vertically. It will not be completely polarized vertically, because only a small fraction of the incident light is reflected, and so a significant amount of horizontally polarized light is refracted.
If you hold your Polaroid sunglasses in front of you and rotate them while looking at blue sky, you will see the sky get bright and dim. This is a clear indication that light scattered by air is partially polarized. [link] helps illustrate how this happens. Since light is a transverse EM wave, it vibrates the electrons of air molecules perpendicular to the direction it is traveling. The electrons then radiate like small antennae. Since they are oscillating perpendicular to the direction of the light ray, they produce EM radiation that is polarized perpendicular to the direction of the ray. When viewing the light along a line perpendicular to the original ray, as in [link] , there can be no polarization in the scattered light parallel to the original ray, because that would require the original ray to be a longitudinal wave. Along other directions, a component of the other polarization can be projected along the line of sight, and the scattered light will only be partially polarized. Furthermore, multiple scattering can bring light to your eyes from other directions and can contain different polarizations.
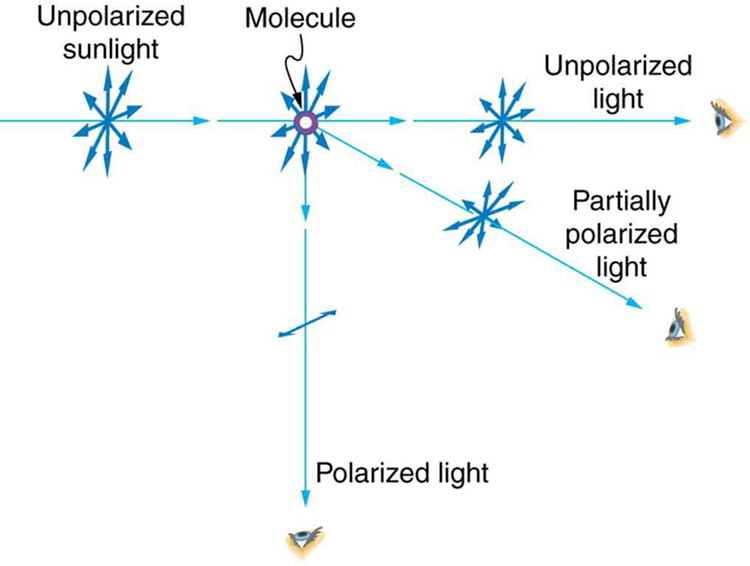
Photographs of the sky can be darkened by polarizing filters, a trick used by many photographers to make clouds brighter by contrast. Scattering from other particles, such as smoke or dust, can also polarize light. Detecting polarization in scattered EM waves can be a useful analytical tool in determining the scattering source.

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?