| << Chapter < Page | Chapter >> Page > |
By the end of this section, you will be able to:
The information presented in this section supports the following AP® learning objectives and science practices:
You have no doubt heard the word pressure being used in relation to blood (high or low blood pressure) and in relation to the weather (high- and low-pressure weather systems). These are only two of many examples of pressures in fluids. Pressure is defined as
where is a force applied to an area that is perpendicular to the force.
Pressure is defined as the force divided by the area perpendicular to the force over which the force is applied, or
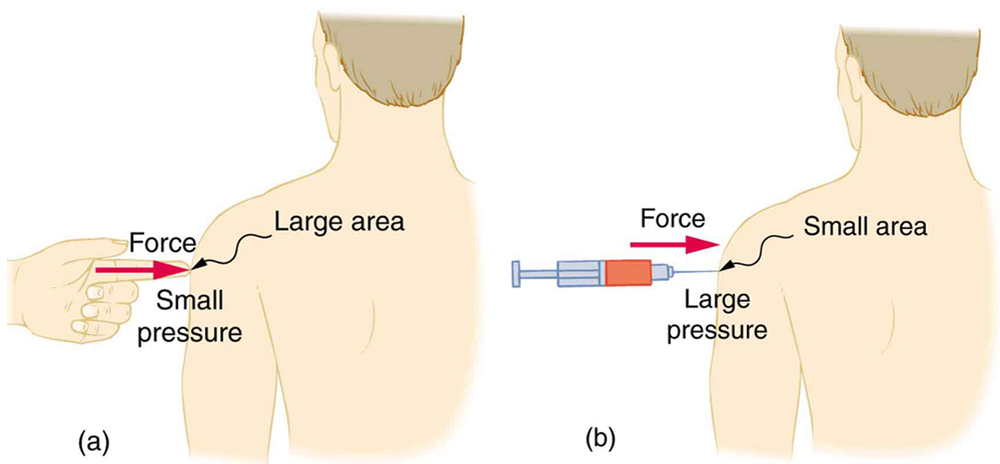
A given force can have a significantly different effect depending on the area over which the force is exerted, as shown in [link] . The SI unit for pressure is the pascal , where
In addition to the pascal, there are many other units for pressure that are in common use. In meteorology, atmospheric pressure is often described in units of millibar (mb), where
Pounds per square inch is still sometimes used as a measure of tire pressure, and millimeters of mercury (mm Hg) is still often used in the measurement of blood pressure. Pressure is defined for all states of matter but is particularly important when discussing fluids.
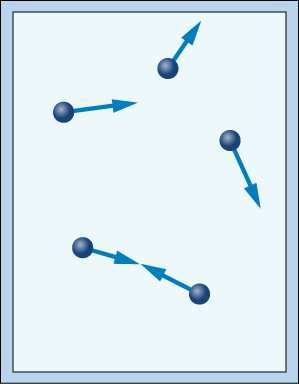
Imagine a closed container full of quickly vibrating gas particles. As the particles rapidly move around the container, they will repeatedly strike each other and the walls of the container.
When the particles strike the walls, a few interesting changes will occur.
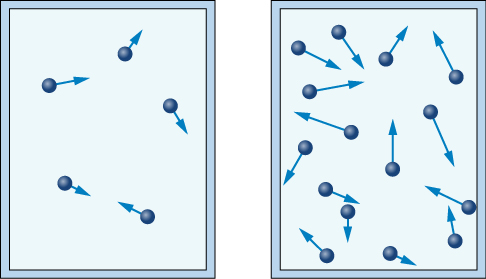
Each time the particles strike the walls of this container, they will apply a force to the container walls. An increase in gas particles will result in more collisions, and a greater force will be applied. The increased force will result in an increased pressure on the container walls, as the areas of the container walls remain constant.
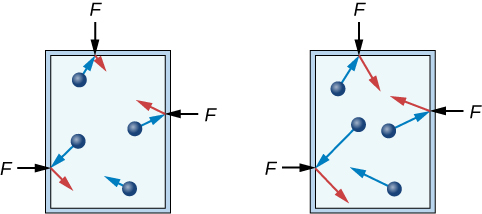
If the speed of the particles is increased, then each particle will experience a greater change in momentum when it strikes a container wall. Just like a fast-moving tennis ball recoiling off a hard surface, the greater the particle's momentum, the more force it will experience when it collides. (For verification, see the impulse-momentum theorem described in Chapter 8.)
However, the more interesting change will be at the wall itself. Due to Newton's third law, it is not only the force on the particle that will increase, but the force on the container will increase as well! While not all particles will move with the same velocity, or strike the wall in the same way, they will experience an average change in momentum upon each collision. The force that these particles impart to the container walls is a good measure of this average change in momentum. Both of these relationships will be useful in Chapter 12, as you consider the ideal gas law. For now, it is good to recognize that laws commonly used to understand macroscopic phenomena can be applied to phenomena at the particle level as well.

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?