| << Chapter < Page | Chapter >> Page > |
Additional general information can be obtained from [link] and the expression for a straight line, .
In this case, the vertical axis is , the intercept is , the slope is , and the horizontal axis is . Substituting these symbols yields
A general relationship for velocity, acceleration, and time has again been obtained from a graph. Notice that this equation was also derived algebraically from other motion equations in Motion Equations for Constant Acceleration in One Dimension .
It is not accidental that the same equations are obtained by graphical analysis as by algebraic techniques. In fact, an important way to discover physical relationships is to measure various physical quantities and then make graphs of one quantity against another to see if they are correlated in any way. Correlations imply physical relationships and might be shown by smooth graphs such as those above. From such graphs, mathematical relationships can sometimes be postulated. Further experiments are then performed to determine the validity of the hypothesized relationships.
Now consider the motion of the jet car as it goes from 165 m/s to its top velocity of 250 m/s, graphed in [link] . Time again starts at zero, and the initial displacement and velocity are 2900 m and 165 m/s, respectively. (These were the final displacement and velocity of the car in the motion graphed in [link] .) Acceleration gradually decreases from to zero when the car hits 250 m/s. The slope of the vs. graph increases until , after which time the slope is constant. Similarly, velocity increases until 55 s and then becomes constant, since acceleration decreases to zero at 55 s and remains zero afterward.
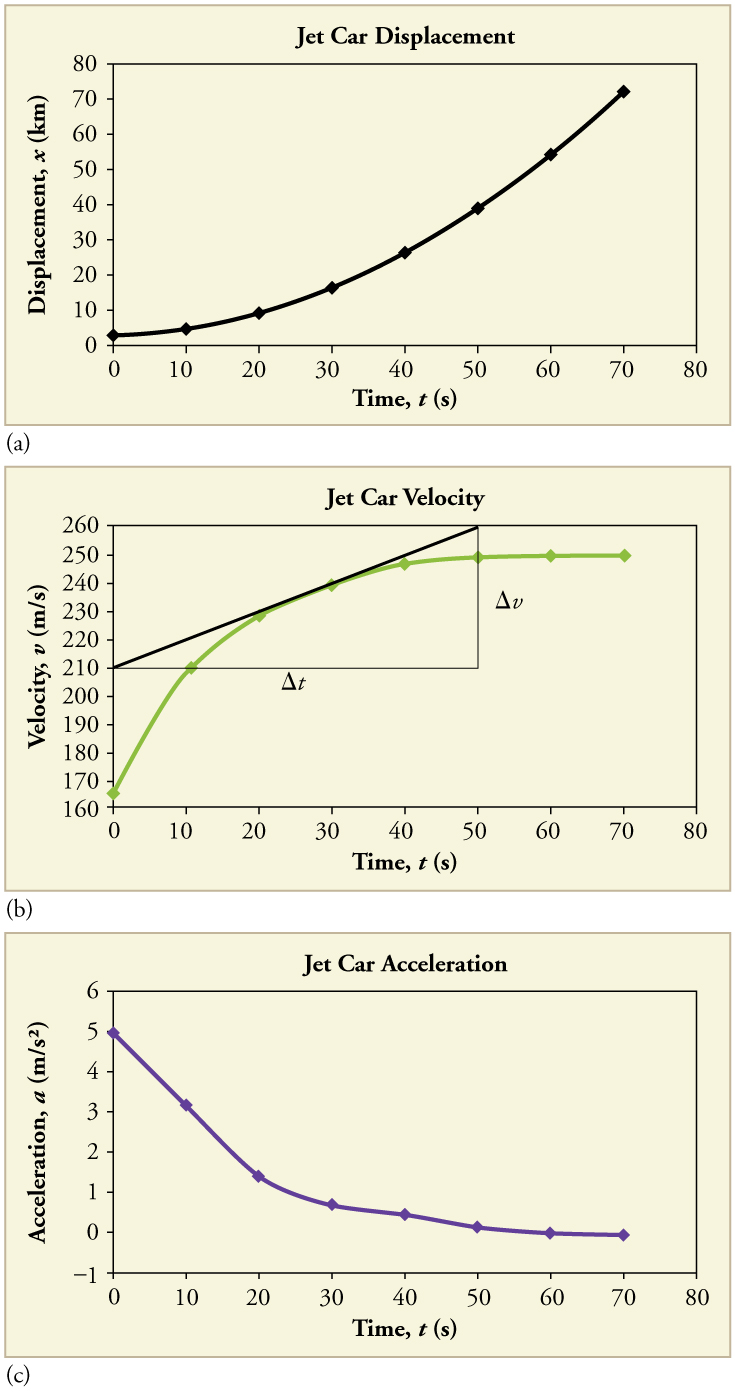
Calculate the acceleration of the jet car at a time of 25 s by finding the slope of the vs. graph in [link] (b).
Strategy
The slope of the curve at is equal to the slope of the line tangent at that point, as illustrated in [link] (b).
Solution
Determine endpoints of the tangent line from the figure, and then plug them into the equation to solve for slope, .
Discussion
Note that this value for is consistent with the value plotted in [link] (c) at .
A graph of displacement versus time can be used to generate a graph of velocity versus time, and a graph of velocity versus time can be used to generate a graph of acceleration versus time. We do this by finding the slope of the graphs at every point. If the graph is linear (i.e., a line with a constant slope), it is easy to find the slope at any point and you have the slope for every point. Graphical analysis of motion can be used to describe both specific and general characteristics of kinematics. Graphs can also be used for other topics in physics. An important aspect of exploring physical relationships is to graph them and look for underlying relationships.

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?