4.4 Newton's third law of motion: symmetry in forces  (Page 3/7)

Getting up to speed: choosing the correct system

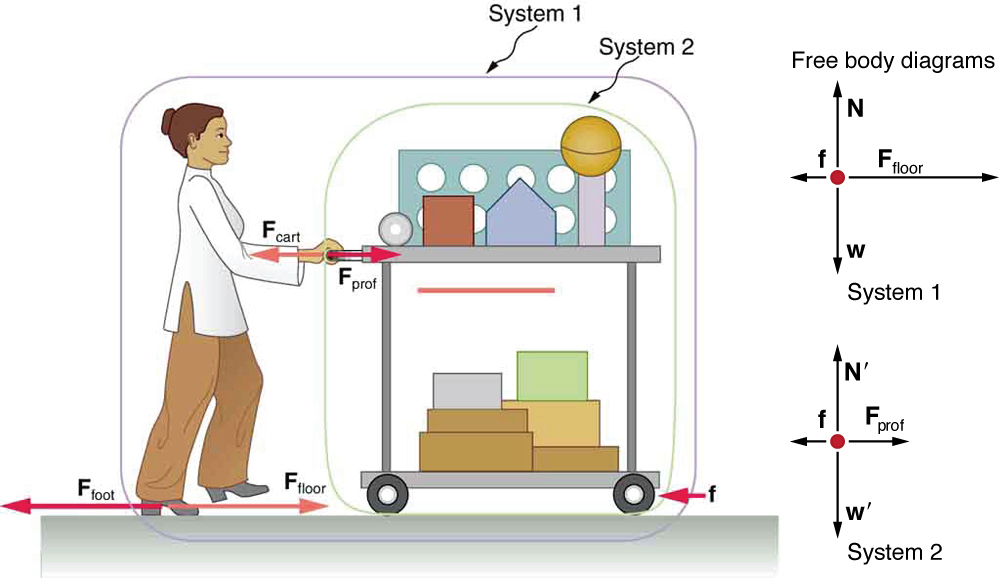
A physics professor pushes a cart of demonstration equipment to a lecture hall, as seen in [link] . Her mass is 65.0 kg, the cart’s is 12.0 kg, and the equipment’s is 7.0 kg. Calculate the acceleration produced when the professor exerts a backward force of 150 N on the floor. All forces opposing the motion, such as friction on the cart’s wheels and air resistance, total 24.0 N.

Strategy

Since they accelerate as a unit, we define the system to be the professor, cart, and equipment. This is System 1 in [link] . The professor pushes backward with a force ${\mathbf{\text{F}}}_{\text{foot}}$ of 150 N. According to Newton’s third law, the floor exerts a forward reaction force ${\mathbf{\text{F}}}_{\text{floor}}$ of 150 N on System 1. Because all motion is horizontal, we can assume there is no net force in the vertical direction. The problem is therefore one-dimensional along the horizontal direction. As noted, $\mathbf{\text{f}}$ opposes the motion and is thus in the opposite direction of ${\mathbf{\text{F}}}_{\text{floor}}$ . Note that we do not include the forces ${\mathbf{\text{F}}}_{\text{prof}}$ or ${\mathbf{\text{F}}}_{\text{cart}}$ because these are internal forces, and we do not include ${\mathbf{\text{F}}}_{\text{foot}}$ because it acts on the floor, not on the system. There are no other significant forces acting on System 1. If the net external force can be found from all this information, we can use Newton’s second law to find the acceleration as requested. See the free-body diagram in the figure.

Solution

Newton’s second law is given by

The net external force on System 1 is deduced from [link] and the discussion above to be

The mass of System 1 is

These values of $F_{\text{net}}$ and $m$ produce an acceleration of

Discussion

None of the forces between components of System 1, such as between the professor’s hands and the cart, contribute to the net external force because they are internal to System 1. Another way to look at this is to note that forces between components of a system cancel because they are equal in magnitude and opposite in direction. For example, the force exerted by the professor on the cart results in an equal and opposite force back on her. In this case both forces act on the same system and, therefore, cancel. Thus internal forces (between components of a system) cancel. Choosing System 1 was crucial to solving this problem.