15.6 Entropy and the second law of thermodynamics: disorder and  (Page 2/10)

Now let us take a look at the change in entropy of a Carnot engine and its heat reservoirs for one full cycle. The hot reservoir has a loss of entropy $\mathrm{\Delta }{S}_{\text{h}}=-Q_{\text{h}}/T_{\text{h}}$ , because heat transfer occurs out of it (remember that when heat transfers out, then $Q$ has a negative sign). The cold reservoir has a gain of entropy $\mathrm{\Delta }{S}_{\text{c}}=Q_{\text{c}}/T_{\text{c}}$ , because heat transfer occurs into it. (We assume the reservoirs are sufficiently large that their temperatures are constant.) So the total change in entropy is

Thus, since we know that $Q_{\text{h}}/T_{\text{h}}=Q_{\text{c}}/T_{\text{c}}$ for a Carnot engine,

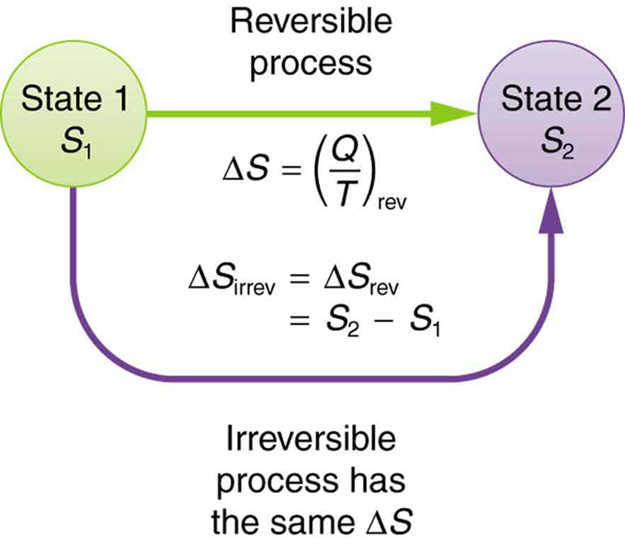
This result, which has general validity, means that the total change in entropy for a system in any reversible process is zero.

The entropy of various parts of the system may change, but the total change is zero. Furthermore, the system does not affect the entropy of its surroundings, since heat transfer between them does not occur. Thus the reversible process changes neither the total entropy of the system nor the entropy of its surroundings. Sometimes this is stated as follows: Reversible processes do not affect the total entropy of the universe. Real processes are not reversible, though, and they do change total entropy. We can, however, use hypothetical reversible processes to determine the value of entropy in real, irreversible processes. The following example illustrates this point.

Entropy increases in an irreversible (real) process

Spontaneous heat transfer from hot to cold is an irreversible process. Calculate the total change in entropy if 4000 J of heat transfer occurs from a hot reservoir at $T_{\text{h}}=\text{600 K}\left(\text{327º C}\right)$ to a cold reservoir at $T_{\text{c}}=\text{250 K}\left(-\text{23º C}\right)$ , assuming there is no temperature change in either reservoir. (See [link] .)

Strategy

How can we calculate the change in entropy for an irreversible process when $\mathrm{\Delta }{S}_{\text{tot}}=\mathrm{\Delta }{S}_{\text{h}}+\mathrm{\Delta }{S}_{\text{c}}$ is valid only for reversible processes? Remember that the total change in entropy of the hot and cold reservoirs will be the same whether a reversible or irreversible process is involved in heat transfer from hot to cold. So we can calculate the change in entropy of the hot reservoir for a hypothetical reversible process in which 4000 J of heat transfer occurs from it; then we do the same for a hypothetical reversible process in which 4000 J of heat transfer occurs to the cold reservoir. This produces the same changes in the hot and cold reservoirs that would occur if the heat transfer were allowed to occur irreversibly between them, and so it also produces the same changes in entropy.

Solution

We now calculate the two changes in entropy using $\mathrm{\Delta }{S}_{\text{tot}}=\mathrm{\Delta }{S}_{\text{h}}+\mathrm{\Delta }{S}_{\text{c}}$ . First, for the heat transfer from the hot reservoir,

And for the cold reservoir,

Thus the total is

Discussion

There is an increase in entropy for the system of two heat reservoirs undergoing this irreversible heat transfer. We will see that this means there is a loss of ability to do work with this transferred energy. Entropy has increased, and energy has become unavailable to do work.