15.6 Entropy and the second law of thermodynamics: disorder and  (Page 3/10)

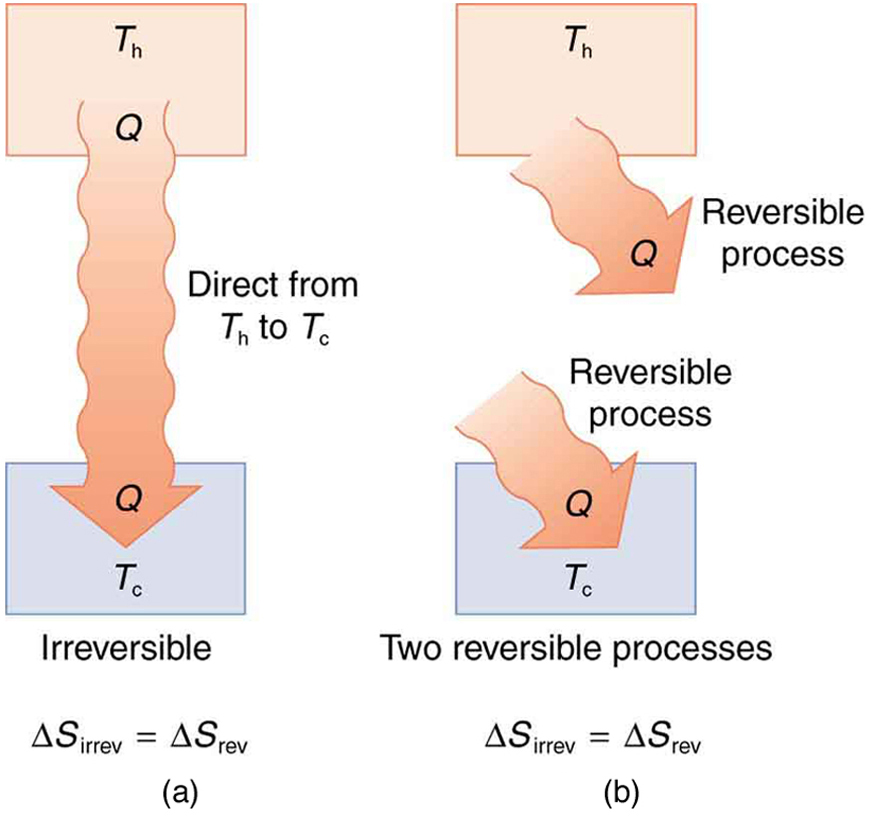
It is reasonable that entropy increases for heat transfer from hot to cold. Since the change in entropy is $Q/T$ , there is a larger change at lower temperatures. The decrease in entropy of the hot object is therefore less than the increase in entropy of the cold object, producing an overall increase, just as in the previous example. This result is very general:

There is an increase in entropy for any system undergoing an irreversible process.

With respect to entropy, there are only two possibilities: entropy is constant for a reversible process, and it increases for an irreversible process. There is a fourth version of the second law of thermodynamics stated in terms of entropy :

The total entropy of a system either increases or remains constant in any process; it never decreases.

For example, heat transfer cannot occur spontaneously from cold to hot, because entropy would decrease.

Entropy is very different from energy. Entropy is not conserved but increases in all real processes. Reversible processes (such as in Carnot engines) are the processes in which the most heat transfer to work takes place and are also the ones that keep entropy constant. Thus we are led to make a connection between entropy and the availability of energy to do work.

Entropy and the unavailability of energy to do work

What does a change in entropy mean, and why should we be interested in it? One reason is that entropy is directly related to the fact that not all heat transfer can be converted into work. The next example gives some indication of how an increase in entropy results in less heat transfer into work.

Less work is produced by a given heat transfer when entropy change is greater

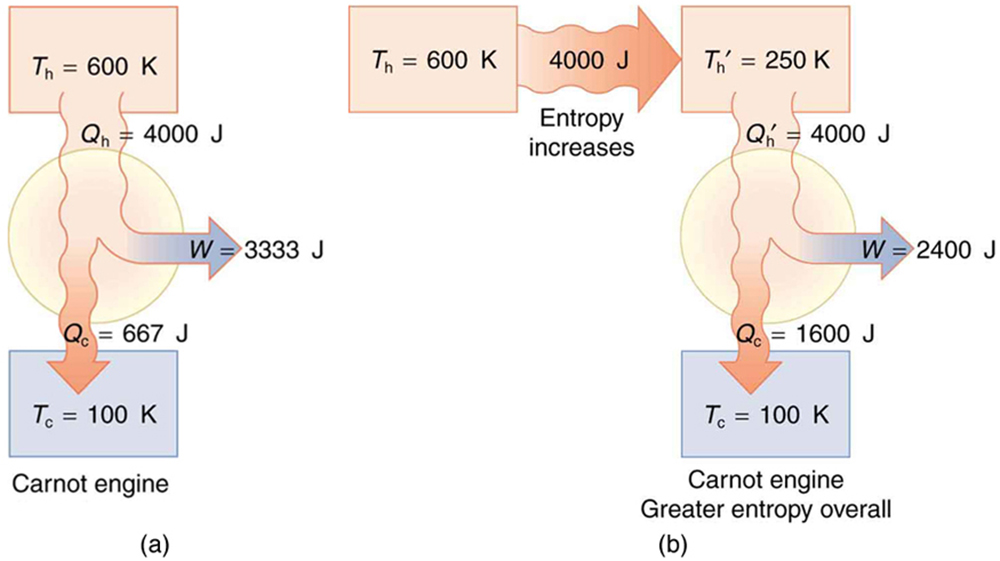
(a) Calculate the work output of a Carnot engine operating between temperatures of 600 K and 100 K for 4000 J of heat transfer to the engine. (b) Now suppose that the 4000 J of heat transfer occurs first from the 600 K reservoir to a 250 K reservoir (without doing any work, and this produces the increase in entropy calculated above) before transferring into a Carnot engine operating between 250 K and 100 K. What work output is produced? (See [link] .)

Strategy

In both parts, we must first calculate the Carnot efficiency and then the work output.

Solution (a)

The Carnot efficiency is given by

${\text{Eff}}_{\text{C}}=1-\frac{T_{\text{c}}}{T_{\text{h}}}\text{.}$

Substituting the given temperatures yields

${\text{Eff}}_{\text{C}}=1-\frac{\text{100 K}}{\text{600 K}}=0\text{.}\text{833}\text{.}$

Now the work output can be calculated using the definition of efficiency for any heat engine as given by

$\text{Eff}=\frac{W}{Q_{\text{h}}}\text{.}$

Solving for $W$ and substituting known terms gives

$\begin{array}{lll}W& =& {\text{Eff}}_{\text{C}}{Q}_{\text{h}}\\ & =& (0.833)(\text{4000}\text{J})=\text{3333 J.}\end{array}$

Solution (b)

Similarly,

${\text{Eff}\prime }_{\text{C}}=1-\frac{T_{\text{c}}}{{\text{T′}}_{\text{c}}}=\text{1}-\frac{\text{100 K}}{\text{250 K}}=\mathrm{0.600,}$

so that

$\begin{array}{lll}W& =& {\text{Eff}\prime }_{\text{C}}{Q}_h\\ & =& (0.600)(\text{4000 J})=\text{2400 J.}\end{array}$

Discussion

There is 933 J less work from the same heat transfer in the second process. This result is important. The same heat transfer into two perfect engines produces different work outputs, because the entropy change differs in the two cases. In the second case, entropy is greater and less work is produced. Entropy is associated with the un availability of energy to do work.

Got questions? Get instant answers now!