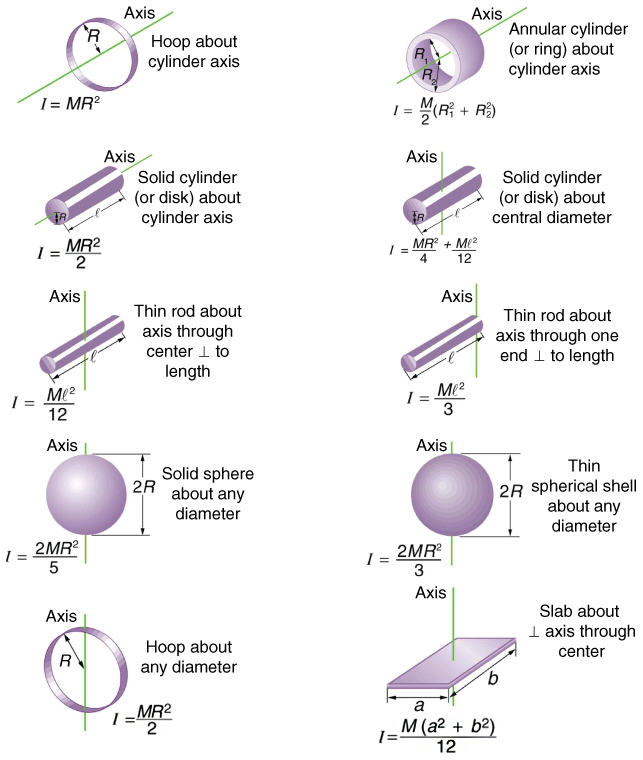
| << Chapter < Page | Chapter >> Page > |
Cut out a circle that has about a 10 cm radius from stiff cardboard. Near the edge of the circle, write numbers 1 to 12 like hours on a clock face. Position the circle so that it can rotate freely about a horizontal axis through its center, like a wheel. (You could loosely nail the circle to a wall.) Hold the circle stationary and with the number 12 positioned at the top, attach a lump of blue putty (sticky material used for fixing posters to walls) at the number 3. How large does the lump need to be to just rotate the circle? Describe how you can change the moment of inertia of the circle. How does this change affect the amount of blue putty needed at the number 3 to just rotate the circle? Change the circle's moment of inertia and then try rotating the circle by using different amounts of blue putty. Repeat this process several times.
In what direction did the circle rotate when you added putty at the number 3 (clockwise or counterclockwise)? In which of these directions was the resulting angular velocity? Was the angular velocity constant? What can we say about the direction (clockwise or counterclockwise) of the angular acceleration? How could you change the placement of the putty to create angular velocity in the opposite direction?
In statics, the net torque is zero, and there is no angular acceleration. In rotational motion, net torque is the cause of angular acceleration, exactly as in Newton's second law of motion for rotation.
Consider the father pushing a playground merry-go-round in [link] . He exerts a force of 250 N at the edge of the 50.0-kg merry-go-round, which has a 1.50 m radius. Calculate the angular acceleration produced (a) when no one is on the merry-go-round and (b) when an 18.0-kg child sits 1.25 m away from the center. Consider the merry-go-round itself to be a uniform disk with negligible retarding friction.
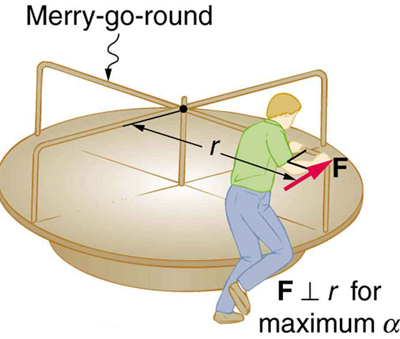
Strategy
Angular acceleration is given directly by the expression :
To solve for , we must first calculate the torque (which is the same in both cases) and moment of inertia (which is greater in the second case). To find the torque, we note that the applied force is perpendicular to the radius and friction is negligible, so that

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?