| << Chapter < Page | Chapter >> Page > |
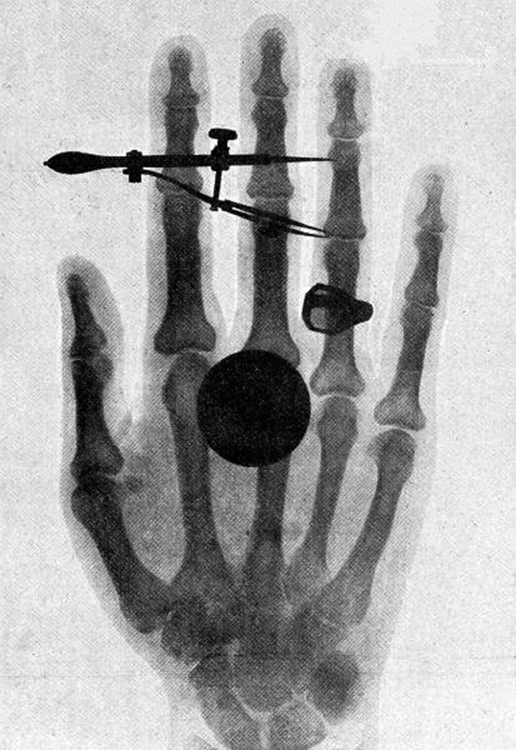
High photon energy also enables rays to penetrate materials, since a collision with a single atom or molecule is unlikely to absorb all the ray’s energy. This can make rays useful as a probe, and they are sometimes used in medical imaging. x rays , as you can see in [link] , overlap with the low-frequency end of the ray range. Since x rays have energies of keV and up, individual x-ray photons also can produce large amounts of ionization. At lower photon energies, x rays are not as penetrating as rays and are slightly less hazardous. X rays are ideal for medical imaging, their most common use, and a fact that was recognized immediately upon their discovery in 1895 by the German physicist W. C. Roentgen (1845–1923). (See [link] .) Within one year of their discovery, x rays (for a time called Roentgen rays) were used for medical diagnostics. Roentgen received the 1901 Nobel Prize for the discovery of x rays.
Once again, we find that conservation of energy allows us to consider the initial and final forms that energy takes, without having to make detailed calculations of the intermediate steps. [link] is solved by considering only the initial and final forms of energy.
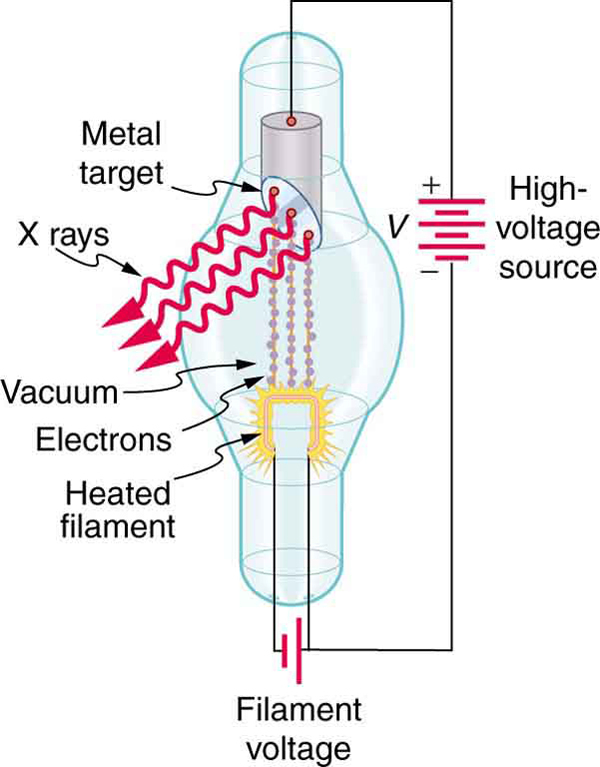
While rays originate in nuclear decay, x rays are produced by the process shown in [link] . Electrons ejected by thermal agitation from a hot filament in a vacuum tube are accelerated through a high voltage, gaining kinetic energy from the electrical potential energy. When they strike the anode, the electrons convert their kinetic energy to a variety of forms, including thermal energy. But since an accelerated charge radiates EM waves, and since the electrons act individually, photons are also produced. Some of these x-ray photons obtain the kinetic energy of the electron. The accelerated electrons originate at the cathode, so such a tube is called a cathode ray tube (CRT), and various versions of them are found in older TV and computer screens as well as in x-ray machines.
Find the maximum energy in eV of an x-ray photon produced by electrons accelerated through a potential difference of 50.0 kV in a CRT like the one in [link] .
Strategy
Electrons can give all of their kinetic energy to a single photon when they strike the anode of a CRT. (This is something like the photoelectric effect in reverse.) The kinetic energy of the electron comes from electrical potential energy. Thus we can simply equate the maximum photon energy to the electrical potential energy—that is, (We do not have to calculate each step from beginning to end if we know that all of the starting energy is converted to the final form )
Solution
The maximum photon energy is , where is the charge of the electron and is the accelerating voltage. Thus,
From the definition of the electron volt, we know , where Gathering factors and converting energy to eV yields
Discussion
This example produces a result that can be applied to many similar situations. If you accelerate a single elementary charge, like that of an electron, through a potential given in volts, then its energy in eV has the same numerical value. Thus a 50.0-kV potential generates 50.0 keV electrons, which in turn can produce photons with a maximum energy of 50 keV. Similarly, a 100-kV potential in an x-ray tube can generate up to 100-keV x-ray photons. Many x-ray tubes have adjustable voltages so that various energy x rays with differing energies, and therefore differing abilities to penetrate, can be generated.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?