| << Chapter < Page | Chapter >> Page > |
Solution for (a)
Constructive interference occurs here when
The smallest constructive thickness thus is
The next thickness that gives constructive interference is , so that
Finally, the third thickness producing constructive interference is , so that
Solution for (b)
For destructive interference , the path length difference here is an integral multiple of the wavelength. The first occurs for zero thickness, since there is a phase change at the top surface. That is,
The first non-zero thickness producing destructive interference is
Substituting known values gives
Finally, the third destructive thickness is , so that
Discussion
If the bubble was illuminated with pure red light, we would see bright and dark bands at very uniform increases in thickness. First would be a dark band at 0 thickness, then bright at 122 nm thickness, then dark at 244 nm, bright at 366 nm, dark at 488 nm, and bright at 610 nm. If the bubble varied smoothly in thickness, like a smooth wedge, then the bands would be evenly spaced.
Another example of thin film interference can be seen when microscope slides are separated (see [link] ). The slides are very flat, so that the wedge of air between them increases in thickness very uniformly. A phase change occurs at the second surface but not the first, and so there is a dark band where the slides touch. The rainbow colors of constructive interference repeat, going from violet to red again and again as the distance between the slides increases. As the layer of air increases, the bands become more difficult to see, because slight changes in incident angle have greater effects on path length differences. If pure-wavelength light instead of white light is used, then bright and dark bands are obtained rather than repeating rainbow colors.
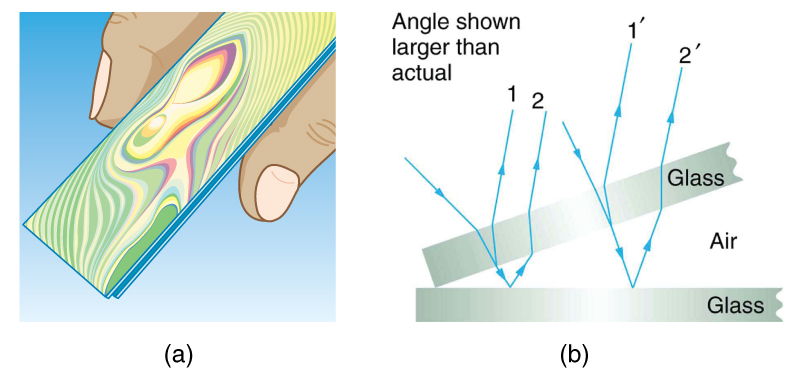
An important application of thin film interference is found in the manufacturing of optical instruments. A lens or mirror can be compared with a master as it is being ground, allowing it to be shaped to an accuracy of less than a wavelength over its entire surface. [link] illustrates the phenomenon called Newton’s rings, which occurs when the plane surfaces of two lenses are placed together. (The circular bands are called Newton’s rings because Isaac Newton described them and their use in detail. Newton did not discover them; Robert Hooke did, and Newton did not believe they were due to the wave character of light.) Each successive ring of a given color indicates an increase of only one wavelength in the distance between the lens and the blank, so that great precision can be obtained. Once the lens is perfect, there will be no rings.


Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?