| << Chapter < Page | Chapter >> Page > |
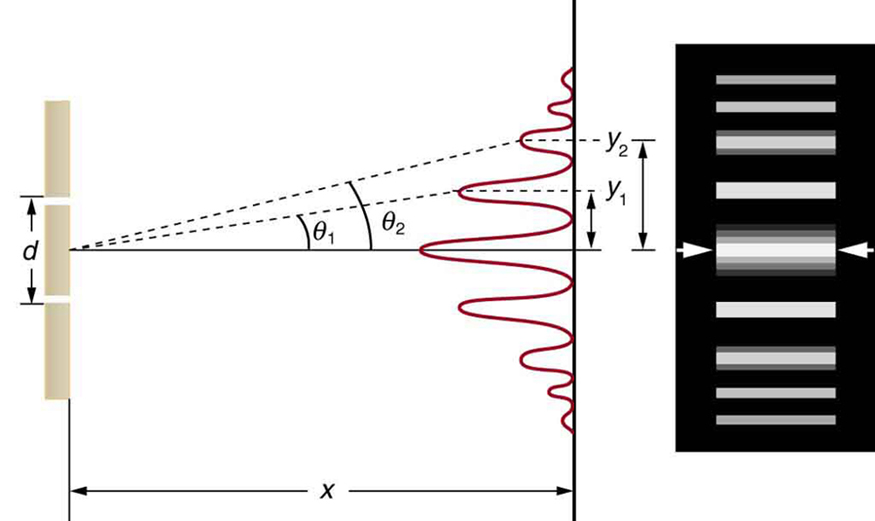
For fixed and , the smaller is, the larger must be, since . This is consistent with our contention that wave effects are most noticeable when the object the wave encounters (here, slits a distance apart) is small. Small gives large , hence a large effect.
Suppose you pass light from a He-Ne laser through two slits separated by 0.0100 mm and find that the third bright line on a screen is formed at an angle of relative to the incident beam. What is the wavelength of the light?
Strategy
The third bright line is due to third-order constructive interference, which means that . We are given and . The wavelength can thus be found using the equation for constructive interference.
Solution
The equation is . Solving for the wavelength gives
Substituting known values yields
Discussion
To three digits, this is the wavelength of light emitted by the common He-Ne laser. Not by coincidence, this red color is similar to that emitted by neon lights. More important, however, is the fact that interference patterns can be used to measure wavelength. Young did this for visible wavelengths. This analytical technique is still widely used to measure electromagnetic spectra. For a given order, the angle for constructive interference increases with , so that spectra (measurements of intensity versus wavelength) can be obtained.
Interference patterns do not have an infinite number of lines, since there is a limit to how big can be. What is the highest-order constructive interference possible with the system described in the preceding example?
Strategy and Concept
The equation describes constructive interference. For fixed values of and , the larger is, the larger is. However, the maximum value that can have is 1, for an angle of . (Larger angles imply that light goes backward and does not reach the screen at all.) Let us find which corresponds to this maximum diffraction angle.
Solution
Solving the equation for gives
Taking and substituting the values of and from the preceding example gives
Therefore, the largest integer can be is 15, or
Discussion
The number of fringes depends on the wavelength and slit separation. The number of fringes will be very large for large slit separations. However, if the slit separation becomes much greater than the wavelength, the intensity of the interference pattern changes so that the screen has two bright lines cast by the slits, as expected when light behaves like a ray. We also note that the fringes get fainter further away from the center. Consequently, not all 15 fringes may be observable.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?