25.6 Image formation by lenses  (Page 8/18)

Image produced by a concave lens

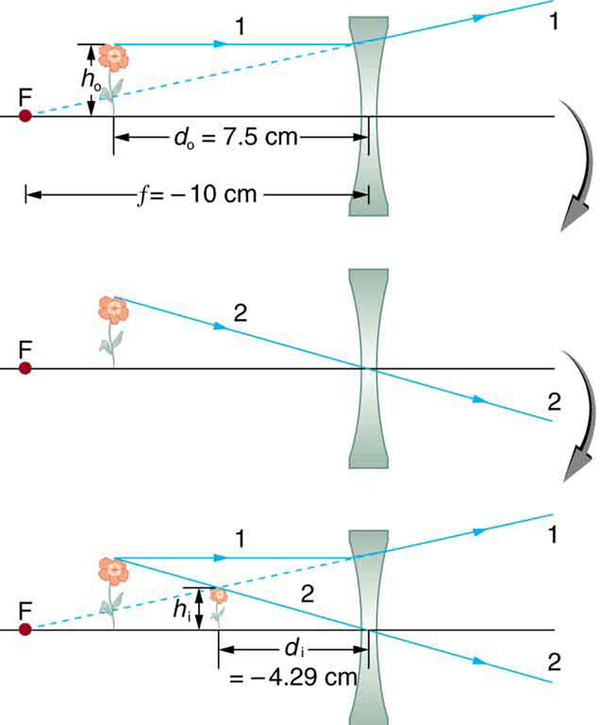
Suppose an object such as a book page is held 7.50 cm from a concave lens of focal length –10.0 cm. Such a lens could be used in eyeglasses to correct pronounced nearsightedness. What magnification is produced?

Strategy and Concept

This example is identical to the preceding one, except that the focal length is negative for a concave or diverging lens. The method of solution is thus the same, but the results are different in important ways.

Solution

To find the magnification $m$ , we must first find the image distance $d_{\text{i}}$ using thin lens equation

or its alternative rearrangement

We are given that $f=\text{–10.0 cm}$ and $d_{\text{o}}=7\text{.}\text{50 cm}$ . Entering these yields a value for $\mathrm{1/}{d}_{\text{i}}$ :

This must be inverted to find $d_{\text{i}}$ :

Or

Now the magnification equation can be used to find the magnification $m$ , since both $d_{\text{i}}$ and $d_{\text{o}}$ are known. Entering their values gives

Discussion

A number of results in this example are true of all case 3 images, as well as being consistent with [link] . Magnification is positive (as predicted), meaning the image is upright. The magnification is also less than 1, meaning the image is smaller than the object—in this case, a little over half its size. The image distance is negative, meaning the image is on the same side of the lens as the object. (The image is virtual.) The image is closer to the lens than the object, since the image distance is smaller in magnitude than the object distance. The location of the image is not obvious when you look through a concave lens. In fact, since the image is smaller than the object, you may think it is farther away. But the image is closer than the object, a fact that is useful in correcting nearsightedness, as we shall see in a later section.