| << Chapter < Page | Chapter >> Page > |
Either way, the universe is destined for thermodynamic equilibrium—maximum entropy. This is often called the heat death of the universe , and will mean the end of all activity. However, whether the universe contracts and heats up, or continues to expand and cools down, the end is not near. Calculations of black holes suggest that entropy can easily continue for at least years.
Entropy is related not only to the unavailability of energy to do work—it is also a measure of disorder. This notion was initially postulated by Ludwig Boltzmann in the 1800s. For example, melting a block of ice means taking a highly structured and orderly system of water molecules and converting it into a disorderly liquid in which molecules have no fixed positions. (See [link] .) There is a large increase in entropy in the process, as seen in the following example.
Find the increase in entropy of 1.00 kg of ice originally at that is melted to form water at .
Strategy
As before, the change in entropy can be calculated from the definition of once we find the energy needed to melt the ice.
Solution
The change in entropy is defined as:
Here is the heat transfer necessary to melt 1.00 kg of ice and is given by
where is the mass and is the latent heat of fusion. for water, so that
Now the change in entropy is positive, since heat transfer occurs into the ice to cause the phase change; thus,
is the melting temperature of ice. That is, . So the change in entropy is
Discussion
This is a significant increase in entropy accompanying an increase in disorder.
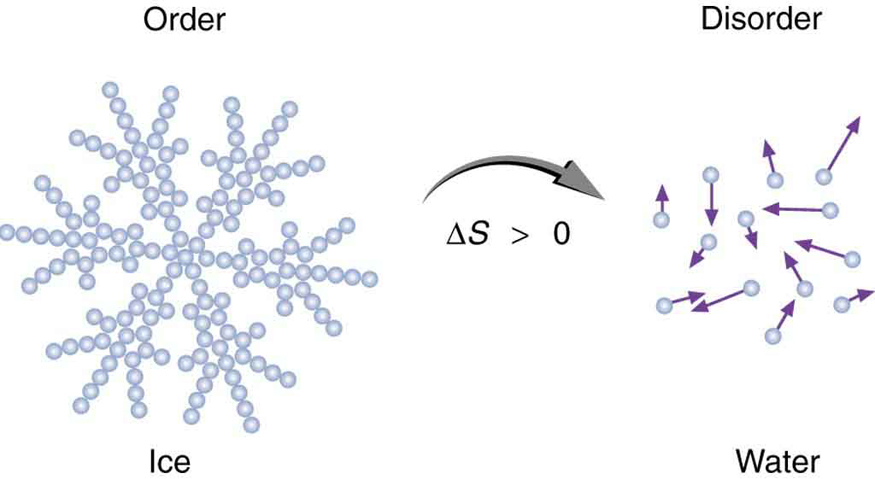
In another easily imagined example, suppose we mix equal masses of water originally at two different temperatures, say and . The result is water at an intermediate temperature of . Three outcomes have resulted: entropy has increased, some energy has become unavailable to do work, and the system has become less orderly. Let us think about each of these results.
First, entropy has increased for the same reason that it did in the example above. Mixing the two bodies of water has the same effect as heat transfer from the hot one and the same heat transfer into the cold one. The mixing decreases the entropy of the hot water but increases the entropy of the cold water by a greater amount, producing an overall increase in entropy.
Second, once the two masses of water are mixed, there is only one temperature—you cannot run a heat engine with them. The energy that could have been used to run a heat engine is now unavailable to do work.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?