1. Home
  2. College physics
  3. Fluid dynamics and its biological
  4. Flow rate and its relation to

12.1 Flow rate and its relation to velocity  (Page 2/6)

<< Chapter < Page
  College physics     Page 2 / 6
Chapter >> Page >
Q 1 = Q 2 A 1 v ¯ 1 = A 2 v ¯ 2 } . size 12{ left none matrix { Q rSub { size 8{1} } =Q rSub { size 8{2} } {} ##A rSub { size 8{1} } {overline {v rSub { size 8{1} } }} =A rSub { size 8{2} } {overline {v rSub { size 8{2} } }} } right rbrace "." } {}

This is called the equation of continuity and is valid for any incompressible fluid. The consequences of the equation of continuity can be observed when water flows from a hose into a narrow spray nozzle: it emerges with a large speed—that is the purpose of the nozzle. Conversely, when a river empties into one end of a reservoir, the water slows considerably, perhaps picking up speed again when it leaves the other end of the reservoir. In other words, speed increases when cross-sectional area decreases, and speed decreases when cross-sectional area increases.

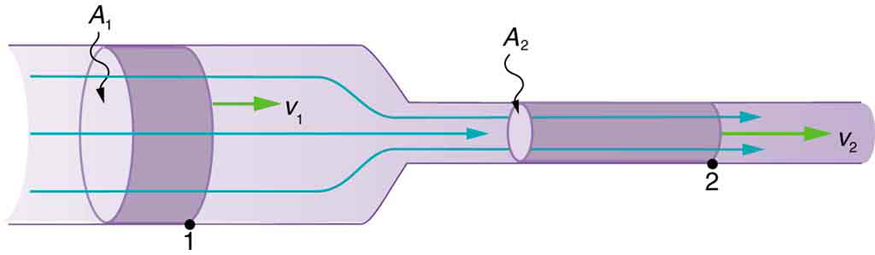
The figure shows a cylindrical tube broad at the left and narrow at the right. The fluid is shown to flow through the cylindrical tube toward right along the axis of the tube. A shaded area is marked on the broader cylinder on the left. A cross section is marked on it as A one. A point one is marked on this cross section. The velocity of the fluid through the shaded area on narrow tube is marked by v one as an arrow toward right. Another shaded area is marked on the narrow cylindrical on the right. The shaded area on narrow tube is longer than the one on broader tube to show that when a tube narrows, the same volume occupies a greater length. A cross section is marked on the narrow cylindrical tube as A two. A point two is marked on this cross section. The velocity of fluid through the shaded area on narrow tube is marked v two toward right. The arrow depicting v two is longer than for v one showing v two to be greater in value than v one.
When a tube narrows, the same volume occupies a greater length. For the same volume to pass points 1 and 2 in a given time, the speed must be greater at point 2. The process is exactly reversible. If the fluid flows in the opposite direction, its speed will decrease when the tube widens. (Note that the relative volumes of the two cylinders and the corresponding velocity vector arrows are not drawn to scale.)

Since liquids are essentially incompressible, the equation of continuity is valid for all liquids. However, gases are compressible, and so the equation must be applied with caution to gases if they are subjected to compression or expansion.

Calculating fluid speed: speed increases when a tube narrows

A nozzle with a radius of 0.250 cm is attached to a garden hose with a radius of 0.900 cm. The flow rate through hose and nozzle is 0.500 L/s. Calculate the speed of the water (a) in the hose and (b) in the nozzle.

Strategy

We can use the relationship between flow rate and speed to find both velocities. We will use the subscript 1 for the hose and 2 for the nozzle.

Solution for (a)

First, we solve Q = A v ¯ size 12{Q=A {overline {v}} } {} for v 1 size 12{v rSub { size 8{1} } } {} and note that the cross-sectional area is A = πr 2 size 12{A=πr rSup { size 8{2} } } {} , yielding

v ¯ 1 = Q A 1 = Q πr 1 2 . size 12{ {overline {v rSub { size 8{1} } }} = { {Q} over {A rSub { size 8{1} } } } = { {Q} over {πr rSub { size 8{1} rSup { size 8{2} } } } } } {}

Substituting known values and making appropriate unit conversions yields

v ¯ 1 = ( 0 . 500 L/s ) ( 10 − 3 m 3 / L ) π ( 9 . 00 × 10 − 3 m ) 2 = 1 . 96 m/s . size 12{ {overline {v rSub { size 8{1} } }} = { { \( 0 "." "500"" L/s" \) \( "10" rSup { size 8{ - 3} } " m" rSup { size 8{3} } /L \) } over {π \( 9 "." "00" times "10" rSup { size 8{ - 3} } " m" \) rSup { size 8{2} } } } =1 "." "96"" m/s"} {}

Solution for (b)

We could repeat this calculation to find the speed in the nozzle v ¯ 2 size 12{ {overline {v rSub { size 8{2} } }} } {} , but we will use the equation of continuity to give a somewhat different insight. Using the equation which states

A 1 v ¯ 1 = A 2 v ¯ 2 , size 12{A rSub { size 8{1} } {overline {v rSub { size 8{1} } }} =A rSub { size 8{2} } {overline {v rSub { size 8{2} } }} } {}

solving for v ¯ 2 size 12{ {overline {v rSub { size 8{2} } }} } {} and substituting πr 2 size 12{πr rSup { size 8{2} } } {} for the cross-sectional area yields

v ¯ 2 = A 1 A 2 v ¯ 1 = πr 1 2 πr 2 2 v ¯ 1 = r 1 2 r 2 2 v ¯ 1 . size 12{ {overline {v rSub { size 8{2} } }} = { {A rSub { size 8{1} } } over {A rSub { size 8{2} } } } {overline {v rSub { size 8{1} } }} = { {πr rSub { size 8{1} rSup { size 8{2} } } } over {πr rSub { size 8{2} rSup { size 8{2} } } } } {overline {v rSub { size 8{1} } }} = { {r rSub { size 8{1} rSup { size 8{2} } } } over {r rSub { size 8{2} rSup { size 8{2} } } } } {overline {v rSub { size 8{1} } }} } {}

Substituting known values,

v ¯ 2 = ( 0 . 900 cm ) 2 ( 0 . 250 cm ) 2 1 . 96 m/s = 25 . 5 m/s . size 12{ {overline {v rSub { size 8{2} } }} = { { \( 0 "." "900"" cm" \) rSup { size 8{2} } } over { \( 0 "." "250"" cm" \) rSup { size 8{2} } } } 1 "." "96"" m/s"="25" "." "5 m/s"} {}

Discussion

A speed of 1.96 m/s is about right for water emerging from a nozzleless hose. The nozzle produces a considerably faster stream merely by constricting the flow to a narrower tube.

Got questions? Get instant answers now!

The solution to the last part of the example shows that speed is inversely proportional to the square of the radius of the tube, making for large effects when radius varies. We can blow out a candle at quite a distance, for example, by pursing our lips, whereas blowing on a candle with our mouth wide open is quite ineffective.

In many situations, including in the cardiovascular system, branching of the flow occurs. The blood is pumped from the heart into arteries that subdivide into smaller arteries (arterioles) which branch into very fine vessels called capillaries. In this situation, continuity of flow is maintained but it is the sum of the flow rates in each of the branches in any portion along the tube that is maintained. The equation of continuity in a more general form becomes
<< Chapter < Page Page > Chapter >>
Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, College physics. OpenStax CNX. Jul 27, 2015 Download for free at http://legacy.cnx.org/content/col11406/1.9
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'College physics' conversation and receive update notifications?

Ask