1. Home
  2. Physics 105: adventures in
  3. W8- fluid drag
  4. Viscosity and laminar flow;

Viscosity and laminar flow; poiseuille’s law  (Page 6/12)

<< Chapter < Page
  Physics 105: adventures in     Page 6 / 12
Chapter >> Page >

Section summary

  • Laminar flow is characterized by smooth flow of the fluid in layers that do not mix.
  • Turbulence is characterized by eddies and swirls that mix layers of fluid together.
  • Fluid viscosity η size 12{η} {} is due to friction within a fluid. Representative values are given in [link] . Viscosity has units of ( N/m 2 ) s size 12{ \( "N/m" rSup { size 8{2} } \) s} {} or Pa ⋅ s size 12{"Pa" cdot s} {} .
  • Flow is proportional to pressure difference and inversely proportional to resistance:
    Q = P 2 − P 1 R . size 12{Q= { {P rSub { size 8{2} } - P rSub { size 8{1} } } over {R} } } {}
  • For laminar flow in a tube, Poiseuille’s law for resistance states that
    R = 8 η l πr 4 . size 12{R= { {8ηl} over {πr rSup { size 8{4} } } } } {}
  • Poiseuille’s law for flow in a tube is
    Q = ( P 2 − P 1 ) π r 4 8 η l . size 12{Q= { { \( P rSub { size 8{2} } - P rSub { size 8{1} } \) π`r rSup { size 8{4} } } over {8ηl} } } {}
  • The pressure drop caused by flow and resistance is given by
    P 2 − P 1 = R Q . size 12{P rSub { size 8{2} } - P rSub { size 8{1} } =R`Q} {}

Conceptual questions

Explain why the viscosity of a liquid decreases with temperature—that is, how might increased temperature reduce the effects of cohesive forces in a liquid? Also explain why the viscosity of a gas increases with temperature—that is, how does increased gas temperature create more collisions between atoms and molecules?

When paddling a canoe upstream, it is wisest to travel as near to the shore as possible. When canoeing downstream, it may be best to stay near the middle. Explain why.

Why does flow decrease in your shower when someone flushes the toilet?

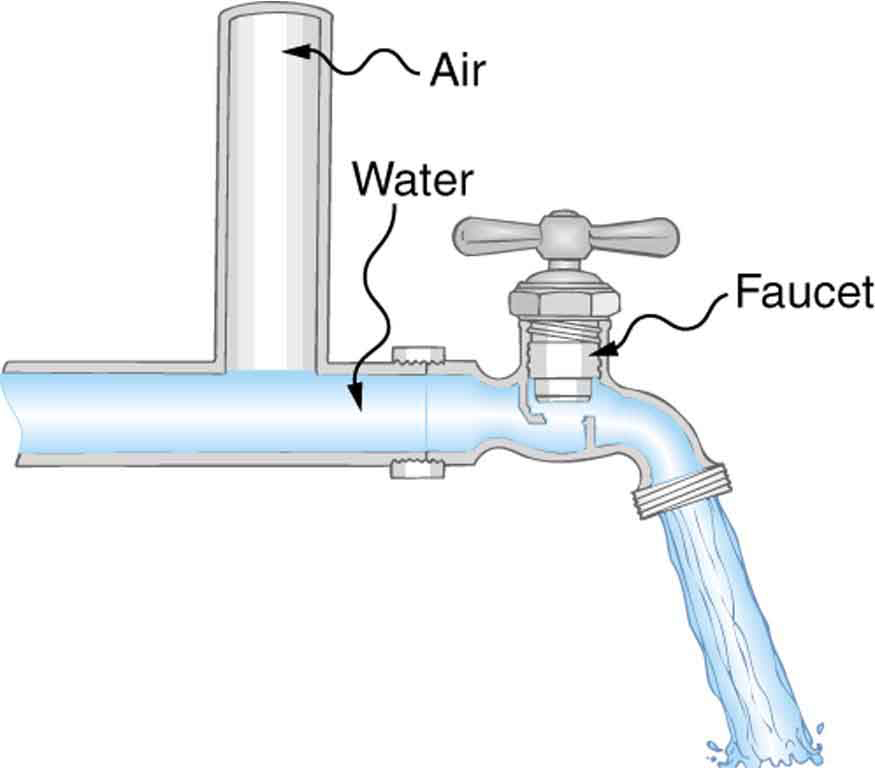
Plumbing usually includes air-filled tubes near water faucets, as shown in [link] . Explain why they are needed and how they work.

The picture shows water gushing out of a water tap. The faucet in the tap is marked. A pipe connected vertically filled with air is shown at an opening on the water pipe before the tap.
The vertical tube near the water tap remains full of air and serves a useful purpose.

Problems&Exercises

(a) Calculate the retarding force due to the viscosity of the air layer between a cart and a level air track given the following information—air temperature is 20º C size 12{"20" rSup { size 8{ circ } } C} {} , the cart is moving at 0.400 m/s, its surface area is 2 . 50 × 10 −2 m 2 size 12{2 "." "50" times "10" rSup { size 8{2} } `m rSup { size 8{2} } } {} , and the thickness of the air layer is 6.00 × 10 − 5 m size 12{6 "." "00" times "10" rSup { size 8{ - 5} } `m} {} . (b) What is the ratio of this force to the weight of the 0.300-kg cart?

(a) 3 . 02 × 10 − 3 N size 12{3 "." "02" times "10" rSup { size 8{ - 3} } " N"} {}

(b) 1 . 03 × 10 − 3 size 12{1 "." "03" times "10" rSup { size 8{ - 3} } } {}

What force is needed to pull one microscope slide over another at a speed of 1.00 cm/s, if there is a 0.500-mm-thick layer of 20º C size 12{"20" rSup { size 12{ circ } } C} {} water between them and the contact area is 8.00 cm 2 size 12{8 "." "00"`"cm" rSup { size 8{2} } } {} ?

A glucose solution being administered with an IV has a flow rate of 4 . 00 cm 3 /min size 12{4 "." "00"`"cm" rSup { size 8{3} } "/min"} {} . What will the new flow rate be if the glucose is replaced by whole blood having the same density but a viscosity 2.50 times that of the glucose? All other factors remain constant.

1 . 60 cm 3 /min size 12{1 "." "60 cm" rSup { size 8{3} } "/min"} {}

The pressure drop along a length of artery is 100 Pa, the radius is 10 mm, and the flow is laminar. The average speed of the blood is 15 mm/s. (a) What is the net force on the blood in this section of artery? (b) What is the power expended maintaining the flow?

A small artery has a length of 1 . 1 × 10 − 3 m size 12{1 "." 1 times "10" rSup { size 8{ - 3} } `m} {} and a radius of 2.5 × 10 − 5 m size 12{2 "." 5 times "10" rSup { size 8{ - 5} } `m} {} . If the pressure drop across the artery is 1.3 kPa, what is the flow rate through the artery? (Assume that the temperature is 37º C size 12{"37"°C} {} .)

8.7 × 10 − 11 m 3 /s size 12{8 "." 7 times "10" rSup { size 8{ - "11"} } `m rSup { size 8{3} } "/s"} {}

Fluid originally flows through a tube at a rate of 100 cm 3 /s size 12{"100"`"cm" rSup { size 8{3} } "/s"} {} . To illustrate the sensitivity of flow rate to various factors, calculate the new flow rate for the following changes with all other factors remaining the same as in the original conditions. (a) Pressure difference increases by a factor of 1.50. (b) A new fluid with 3.00 times greater viscosity is substituted. (c) The tube is replaced by one having 4.00 times the length. (d) Another tube is used with a radius 0.100 times the original. (e) Yet another tube is substituted with a radius 0.100 times the original and half the length, and the pressure difference is increased by a factor of 1.50.
<< Chapter < Page Page > Chapter >>
Practice Key Terms 5

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Physics 105: adventures in physics. OpenStax CNX. Dec 02, 2015 Download for free at http://legacy.cnx.org/content/col11916/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Physics 105: adventures in physics' conversation and receive update notifications?

Ask