| << Chapter < Page | Chapter >> Page > |
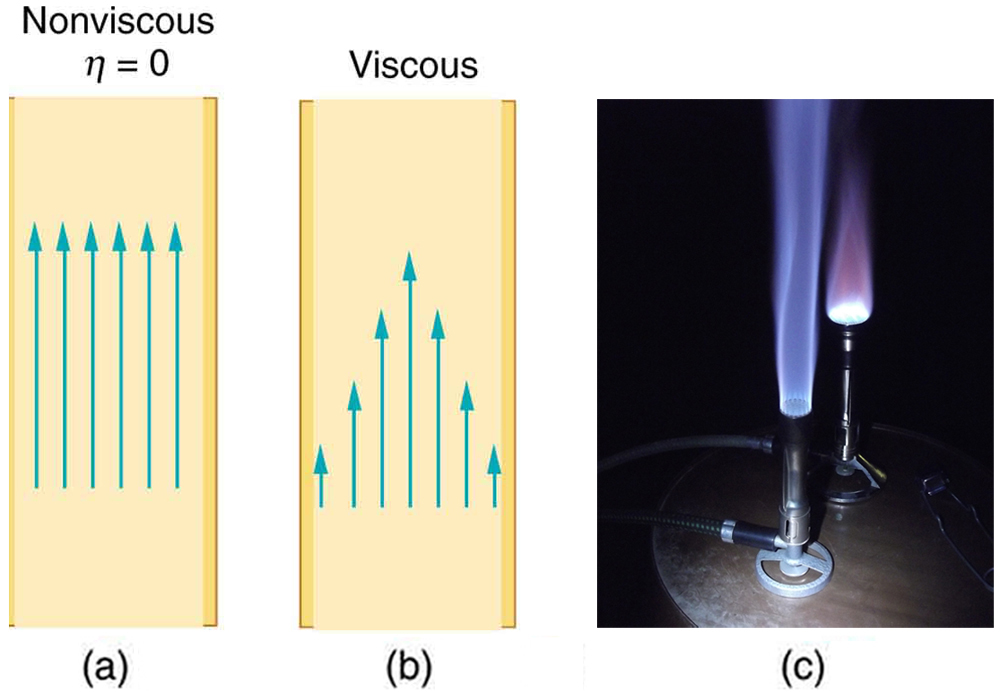
If viscosity is zero, the fluid is frictionless and the resistance to flow is also zero. Comparing frictionless flow in a tube to viscous flow, as in [link] , we see that for a viscous fluid, speed is greatest at midstream because of drag at the boundaries. We can see the effect of viscosity in a Bunsen burner flame, even though the viscosity of natural gas is small.
The resistance to laminar flow of an incompressible fluid having viscosity through a horizontal tube of uniform radius and length , such as the one in [link] , is given by
This equation is called Poiseuille’s law for resistance after the French scientist J. L. Poiseuille (1799–1869), who derived it in an attempt to understand the flow of blood, an often turbulent fluid.
Let us examine Poiseuille’s expression for to see if it makes good intuitive sense. We see that resistance is directly proportional to both fluid viscosity and the length of a tube. After all, both of these directly affect the amount of friction encountered—the greater either is, the greater the resistance and the smaller the flow. The radius of a tube affects the resistance, which again makes sense, because the greater the radius, the greater the flow (all other factors remaining the same). But it is surprising that is raised to the fourth power in Poiseuille’s law. This exponent means that any change in the radius of a tube has a very large effect on resistance. For example, doubling the radius of a tube decreases resistance by a factor of .
Taken together, and give the following expression for flow rate:
This equation describes laminar flow through a tube. It is sometimes called Poiseuille’s law for laminar flow, or simply Poiseuille’s law .
Suppose the flow rate of blood in a coronary artery has been reduced to half its normal value by plaque deposits. By what factor has the radius of the artery been reduced, assuming no turbulence occurs?
Strategy
Assuming laminar flow, Poiseuille’s law states that
We need to compare the artery radius before and after the flow rate reduction.
Solution
With a constant pressure difference assumed and the same length and viscosity, along the artery we have
So, given that , we find that .
Therefore, , a decrease in the artery radius of 16%.
Discussion
This decrease in radius is surprisingly small for this situation. To restore the blood flow in spite of this buildup would require an increase in the pressure difference of a factor of two, with subsequent strain on the heart.
| Fluid | Temperature (ºC) | Viscosity |
|---|---|---|
| Gases | ||
| Air | 0 | 0.0171 |
| 20 | 0.0181 | |
| 40 | 0.0190 | |
| 100 | 0.0218 | |
| Ammonia | 20 | 0.00974 |
| Carbon dioxide | 20 | 0.0147 |
| Helium | 20 | 0.0196 |
| Hydrogen | 0 | 0.0090 |
| Mercury | 20 | 0.0450 |
| Oxygen | 20 | 0.0203 |
| Steam | 100 | 0.0130 |
| Liquids | ||
| Water | 0 | 1.792 |
| 20 | 1.002 | |
| 37 | 0.6947 | |
| 40 | 0.653 | |
| 100 | 0.282 | |
| Whole blood The ratios of the viscosities of blood to water are nearly constant between 0°C and 37°C. | 20 | 3.015 |
| 37 | 2.084 | |
| Blood plasma See note on Whole Blood. | 20 | 1.810 |
| 37 | 1.257 | |
| Ethyl alcohol | 20 | 1.20 |
| Methanol | 20 | 0.584 |
| Oil (heavy machine) | 20 | 660 |
| Oil (motor, SAE 10) | 30 | 200 |
| Oil (olive) | 20 | 138 |
| Glycerin | 20 | 1500 |
| Honey | 20 | 2000–10000 |
| Maple Syrup | 20 | 2000–3000 |
| Milk | 20 | 3.0 |
| Oil (Corn) | 20 | 65 |

Notification Switch
Would you like to follow the 'Physics 105: adventures in physics' conversation and receive update notifications?