| << Chapter < Page | Chapter >> Page > |
A Theorem on the Log Canonical Threshold Mike Clendenen, Ira Jamshidi, Lauren Kirton, David Lax Dr. Hassett, Dr. Varilly S. Li, Z. Li, B. Waters NSF grant 0739420 July 16, 2009
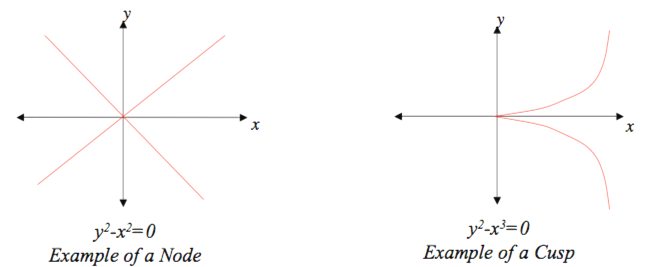
In the study of solutions to polynomial equations, there are points of interest called singularities. A singularity on a plane curve is a point that does not look locally like the graph of a function (see Figures 1). There is a number associated with every singularity called the log canonical threshold (LCT) that carries some information about the singularity. In a sense, this number is a measure of how bad a singularity is. A higher LCT corresponds to a “nicer” singularity. For example, the node below has LCT 1 and the cusp has LCT . This corresponds to the notion that the node seems to be a nicer singularity.
In this paper we examine the LCT of polynomials of the form . Such polynomials have a singularity at the origin when . This is an important case to understand since many singularities can be related to a singularity of this form. We give an elementary proof of the following theorem:
Theorem 1.1 .
This is a special case of J. Igusa's theorem from 1977. In his notation for his theorem, this is the case where the Puiseux series of a plane curve is of the form: [link] Section 1. Before giving the proof of Theorem [link] we will first define the algebro-geometric terms necessary to understand the theorem and then review concepts from continued fractions which are useful in the proof of the theorem.
In this section we give precise definitions for some of the algebro-geometric concepts mentioned in "Introduction" ; we establish some notation along the way. Throughout, we work over the field of complex numbers.
Definition 2.1 A plane curve is the set of all points in the affine plane such that a given function is zero.
Definition 2.2 A singularity is a point on a plane curve where all of the partial derivatives vanish, that is, a point such that . A singulariy is called an isolated singularity if in some small neighborhood of the point, it is the only singularity of the curve.
Example 2.3 Let . The partial derivatives of f are given by
Thus, at the origin, , and is a singularity of . One can check that this is an isolated singularity.
Given a singularity, we can “resolve” it into slopes by implementing a series of substitutions of a particular kind and graphing the resulting curves. For example, a curve in x and y can be resolved by the substitutions or , where t and s represent slopes of lines through the singularity. This process is called blowing-up , and each stage at which a new substitution is introduced is known as a blow-up . The axes we use in the blow-up diagrams are called exceptional divisors , and can be thought of as “slope axes” at the point of blowing-up. We denote the exceptional divisor of the blow-up as E i . We continue the process of blowing-up until we achieve a normal crossings , which is a result of blowing-up where the graph has no singularities and meets the exceptional divisors at unique intersections, without being tangent to an exceptional divisor at any point.

Notification Switch
Would you like to follow the 'The art of the pfug' conversation and receive update notifications?