Uniform circular motion

Uniform circular motion denotes motion of a particle along a circular arc or a circle with constant speed. This statement, as a matter of fact, can be construed as the definition of uniform circular motion.

Requirement of uniform circular motion

The uniform circular motion represents the basic form of rotational motion in the same manner as uniform linear motion represents the basic form of translational motion. They, however, are different with respect to the requirement of force to maintain motion.

Uniform linear motion is the reflection of the inherent natural tendency of all natural bodies. This motion by itself is the statement of Newton’s first law of motion : an object keeps moving with its velocity unless there is net external force. Thus, uniform linear motion indicates “absence” of force.

On the other hand, uniform circular motion involves continuous change in the direction of velocity without any change in its magnitude (v). A change in the direction of velocity is a change in velocity ( v ). It means that an uniform circular motion is associated with an acceleration and hence force. Thus, uniform circular motion indicates “presence” of force.

Let us now investigate the nature of force required to maintain uniform circular motion. We know that a force acting in the direction of motion changes only the magnitude of velocity. A change in the direction of motion, therefore, requires that velocity of the particle and force acting on it should be at an angle. However, such a force, at an angle with the direction of motion, would have a component along the direction of velocity as well and that would change the magnitude of the motion.

Change of direction

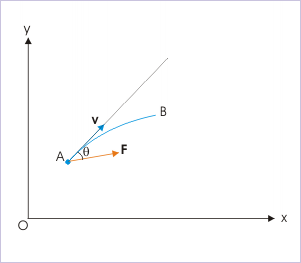
In order that there is no change in the magnitude of velocity, the force should have zero component along the direction of velocity. It is possible only if the force be perpendicular to the direction of velocity such that its component in the direction of velocity is zero (Fcos90° = 0). Precisely, this is the requirement for a motion to be uniform circular motion.

Uniform circular motion

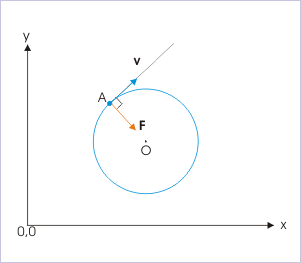
In plain words, uniform circular motion (UCM) needs a force, which is always perpendicular to the direction of velocity. Since the direction of velocity is continuously changing, the direction of force, being perpendicular to velocity, should also change continously.

The direction of velocity along the circular trajectory is tangential. The perpendicular direction to the circular trajectory is, therefore, radial direction. It implies that force (and hence acceleration) in uniform direction motion is radial. For this reason, acceleration in UCM is recognized to seek center i.e. centripetal (seeking center).

This fact is also validated by the fact that the difference of velocity vectors, whose time rate gives acceleration, at two instants (Δ v ) is radial.