Did you know?
|
|
is a
proper fraction. The numerator is smaller than the denominator. |
|
|
is an
improper fraction. The numerator is bigger than the denominator. |
|
|
is a
mixed number . A mixed number is always bigger than 1 and consists of a whole number (1) plus a fraction (
). |
Activity 3:
To calculate by means of computations that are suitable to be used in adding ordinary fractions [lo 1.8.3]
1. Can you still remember how to add fractions? Let us see. Work together with a friend. Take turns to say the answers. Choose any two fractions and add them. Give your answer first as an improper fraction and then as a mixed number.
Ask your teacher’s help if you struggle.
1.1
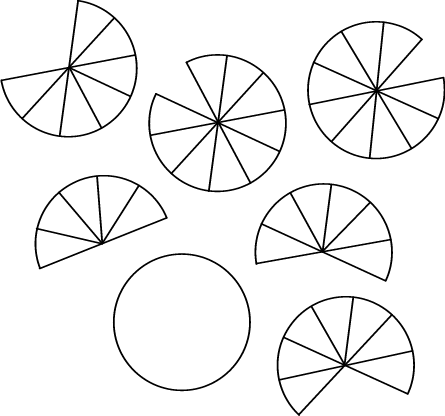 |
1.2
 |
Activity 4:
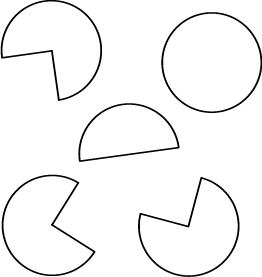
1. Look carefully at the following questions and then complete them as neatly as possible.
EQUIVALENT FRACTIONS
| 1.1 Colour
of the figure in blue: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1.2 Colour
of the figure in green: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1.3 Colour
of the figure in yellow: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1.4 Colour
of the figure in red: |
Did you know?
We call fractions that are equal in size,
equivalent fractions. The word equivalent means
‘the same as’ . Thus the fractions are equal.
Do you remember?
| 1 unit |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. The following activity will prepare you for the addition and subtraction of fractions. Use your knowledge of equivalent fractions and answer the following. Where you are in doubt, use the diagram above.
2.1:
2.2:
2.3:
2.4:
2.5:
2.6:
2.7:
2.8:
2.9:
2.10:
Assessment
| Learning outcomes(LOs) |
|
| LO 1 |
| Numbers, Operations and RelationshipsThe learner is able to recognise, describe and represent numbers and their relationships, and counts, estimates, calculates and checks with competence and confidence in solving problems. |
| Assessment standards(ASs) |
|
| We know this when the learner: |
| 1.1 counts forwards and backwards fractions; |
| 1.2 describes and illustrates various ways of writing numbers in different cultures (including local) throughout history; |
1.3 recognises and represents the following numbers in order to describe and compare them:
- common fractions to at least twelfths;
|
| 1.5 recognises and uses equivalent forms of the numbers listed above, including: |
| 1.5.1 common fractions with denominators that are multiples of each other; |
1.6 solves problems in context including contexts that may be used to build awareness of other Learning Areas, as well as human rights, social, economic and environmental issues such as:
- financial (including buying and selling, profit and loss, and simple budgets);
|
| LO 5 |
| Data handlingThe learner will be able to collect, summarise, display and critically analyse data in order to draw conclusions and make predictions, and to interpret and determine chance variation. |
| We know this when the learner: |
| 5.3 organises and records data using tallies and tables; |
| 5.5 draws a variety of graphs to display and interpret data (ungrouped) including:
|
Memorandum
ACTIVITY 1
1.1 Equal parts of a whole
1.2 Nominator
1.3
1.4 Say in how many equal parts the whole is divided
1.5 Smaller
1.6 Nominator
1.7 Equivalents
1.8 Larger
1.9 Say with how many equal parts I work / are coloured in
1.10 Divide the nominator and denominator by the same number
2. 2.1 b and c
2.4 Not equal parts
2.5 (i)
(ii)
/
(iii)
/
(iv)
(v)
(vi)
(vii)
/
(viii)
/
(ix)
(x)
(xi)
ACTIVITY 2
1.
| B |
8 |
1 |
|
7 |
|
| C |
6 |
1 |
|
5 |
|
| D |
8 |
1 |
|
7 |
|
| E |
3 |
1 |
|
2 |
|
| F |
12 |
6 |
/
|
6 |
/
|
| G |
16 |
8 |
/
|
8 |
/
|
| H |
16 |
4 |
/
|
12 |
/
|
| I |
8 |
2 |
/
|
6 |
/
|
| J |
12 |
6 |
/
|
6 |
/
|
| K |
8 |
2 |
/
|
6 |
/
|
ACTIVITY 4
1.5 Fractions all equal
1.6
=
=
=
2. 2.1
2.6
2.2
2.7
2.3
2.8
2.4
2.9
2.5
2.10
3. 3.1
3.4
3.2
3.5
3.3
3.6
4.
=
=
=
=
=
=


