Special theory of relativity  (Page 6/9)

On the other hand, speed of light in vacuum is invariant in inertial references (though it is not invariant in accelerated references). As such, it can be used as a parameter to measure “time” and “distance”. A linear distance, for example, can be expressed in terms of “time” taken by light to cover a given distance. Alternatively, a particular time interval can be expressed in terms of “linear distance” covered by the light in a given time.

The official measure of speed of light in vacuum is as given here :

c = 299,792,458 meters/second

Galilean transformation

The transforms are mathematical constructs which allow us to convert one set of spatial (x,y,z) and time (t) measurements in one frame of reference to another frame of reference based on certain physical principle or law. Our current context is limited to inertial frames of reference. Therefore, we shall study transforms which refer to inertial frames of reference. Here, we shall study Galilean and Lorentz transforms. The Galilean transform encapsulates the ideas of non-relativistic mechanics whereas Lorentz transform encapsulates the ideas of relativistic mechanics.

The concepts of a transform, physical laws and inertial frames of reference are entangled with each other. The physical laws are required to be valid across all inertial frames of references.

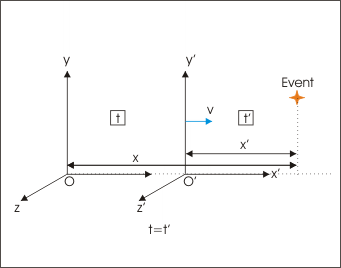
Galilean transform gives the relation between two inertial systems which are moving at a constant velocity with respect to each other. If space (co-ordinates) and time values in one reference are known, then we can find out space and time values using Galilean transform in another reference which is moving at a constant velocity “v’ with respect to first in x-direction. Let two inertial reference systems are denoted by unprimed and primed variables and their spatial origins coincide at t = t' = 0. Then, space (x',y',z') and time (t') co-ordinates of a "single arbitrary event" in primed inertial reference is related to space (x,y,z) and time (t) of unprimed inertial reference as :

Galilean transformation

$$x\prime =x-vt$$ $$y\prime =y$$ $$z\prime =z$$ $$t\prime =t$$

We can also express unprimed variables in terms of primed variable by solving for unprimed variable as :

$$x=x\prime +vt$$ $$y=y\prime$$ $$z=z\prime$$ $$t=t\prime$$

The most important aspect of Galilean transform is the last equation, t’ = t, denoting that time is an invariant for inertial frames of references. The constancy of time across inertial frames of reference is the key consideration here. With the advent of special theory of relativity, however, this transform is considered as a restricted case as it is valid for small relative speed,v, only. At higher values of relative speed “v”, we need to employ Lorentz transform in accordance with special theory of relativity such that speed of light in vacuum is constant in all inertial references.

Further, we get the equation for the velocities of a particle or object at position "x" or "x'" in the unprimed and primed references respectively by differentiating first equation of the transform,