| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
Suppose three friends are going to the movies. They each need that is, dollars and quarter. How much money do they need all together? You can think about the dollars separately from the quarters.


They need times so and times quarter, so cents. In total, they need
If you think about doing the math in this way, you are using the Distributive Property.
If are real numbers, then
Back to our friends at the movies, we could show the math steps we take to find the total amount of money they need like this:
In algebra, we use the Distributive Property to remove parentheses as we simplify expressions. For example, if we are asked to simplify the expression the order of operations says to work in the parentheses first. But we cannot add and since they are not like terms. So we use the Distributive Property, as shown in [link] .
Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in [link] would look like this:
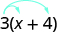
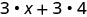
The distributive property can be used to simplify expressions that look slightly different from Here are two other forms.
| If are real numbers, then | |
| Other forms: |
|
Do you remember how to multiply a fraction by a whole number? We’ll need to do that in the next two examples.
Using the Distributive Property as shown in the next example will be very useful when we solve money applications later.
In the next example we’ll multiply by a variable. We’ll need to do this in a later chapter.
Simplify:
|
| |
| Distribute. |
|
| Multiply. |
|
Notice that we wrote We can do this because of the Commutative Property of Multiplication. When a term is the product of a number and a variable, we write the number first.
The next example will use the ‘backwards’ form of the Distributive Property,

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?