| << Chapter < Page | Chapter >> Page > |
Vì hầu hết khối kim loại đều có cùng điện thế V0 tương ứng với thế năng U0=-eV0 nên ta có thể giả sử khối kim loại là một khối đẳng thế V0. Nhưng điện thế tùy thuộc vào một hằng số cộng nên ta có thể chọn V0 làm điện thế gốc (V0=0V). Gọi EB là chiều cao của rào thế năng giữa bên trong và bên ngoài kim loại. Một điện tử bên trong khối kim loại muốn vượt ra ngoài phải có ít nhất một năng lượng U=EB, vì vậy ta cần phải biết sự phân bố của điện tử theo năng lượng.
Gọi nE= là số điện tử trong một đơn vị thể tích có năng lượng từ E đến E+E. Theo định nghĩa, mật độ điện tử trung bình có năng lượng từ E đến E+E là tỉ số . Giới hạn của tỉ số này khi gọi là mật độ điện tử có năng lượng E.
Ta có:
Vậy,
Do đó, nếu ta biết được hàm số ta có thể suy ra được số điện tử có năng lượng trong khoảng từ E đến E+dE bằng biểu thức (2). Ta thấy rằng (E) chính là số trạng thái năng lượng E đã bị điện tử chiếm. Nếu gọi n(E) là số trạng thái năng lượng có năng lượng E mà điện tử có thể chiếm được. Người ta chứng minh được rằng: tỉ số bằng một hàm số f(E), có dạng:
Trong đó, K=1,381.10-23 J/0K (hằng số Boltzman)
EF năng lượng Fermi, tùy thuộc vào bản chất kim loại.
Mức năng lượng này nằm trong dải cấm.
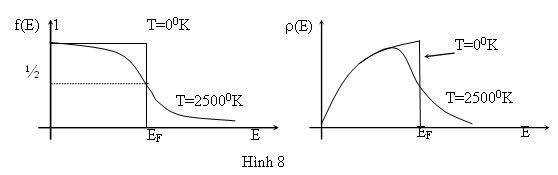
Ở nhiệt độ rất thấp (T00K)
Nếu E<EF, ta có f(E)=1
Nếu E>EF, ta có f(E)=0
Vậy f(E) chính là xác suất để tìm thấy điện tử có năng lượng E ở nhiệt độ T.
Hình sau đây là đồ thị của f(E) theo E khi T00K và khi T=2.5000K.
Ta chấp nhận rằng:
là hằng số tỉ lệ.
Lúc đó, mật độ điện tử có năng lượng E là:
Hình trên là đồ thị của (E) theo E tương ứng với nhiệt độ T=00K và T=2.5000K.
Ta thấy rằng hàm (E) biến đổi rất ít theo nhiệt độ và chỉ biến đổi trong vùng cận của năng lượng EF. Do đó, ở nhiệt độ cao (T=2.5000K) có một số rất ít điện tử có năng lượng lớn hơn EF, hầu hết các điện tử đều có năng lượng nhỏ hơn EF. Diện tích giới hạn bởi đường biểu diễn của (E) và trục E cho ta số điện tử tự do n chứa trong một đơn vị thể tích.
(Để ý là f(E)=1 và T=00K)
Từ đây ta suy ra năng lượng Fermi EF
Nếu ta dùng đơn vị thể tích là m3 và đơn vị năng lượng là eV thì có trị số là:
= 6,8.1027
Do đó,
Nếu biết được khối lượng riêng của kim loại và số điện tử tự do mà mỗi nguyên tử có thể nhả ra, ta tính được n và từ đó suy ra EF. Thông thường EF<10eV.
Thí dụ, khối lượng riêng của Tungsten là d = 18,8g/cm3, nguyên tử khối là A = 184, biết rằng mỗi nguyên tử cho v = 2 điện tử tự do. Tính năng lượng Fermi.
Giải: Khối lượng mỗi cm3 là d, vậy trong mỗt cm3 ta có một số nguyên tử khối là d/A. Vậy trong mỗi cm3, ta có số nguyên tử thực là:
với A0 là số Avogadro (A0 = 6,023.1023)
Mỗi nguyên tử cho v = 2 điện tử tự do, do đó số điện tử tự do trong mỗi m3 là:
Với Tungsten, ta có:
điện tử/m3
Ta thấy rằng ở nhiệt độ thấp (T 00K), năng lượng tối đa của điện tử là EF (E<EF<EB), do đó, không có điện tử nào có năng lượng lớn hơn rào thế năng EB, nghĩa là không có điện tử nào có thể vượt ra ngoài khối kim loại. Muốn cho điện tử có thể vượt ra ngoài, ta phải cung cấp cho điện tử nhanh nhất một năng lượng là:
EW = EB-EF
EW được gọi là công ra của kim loại.
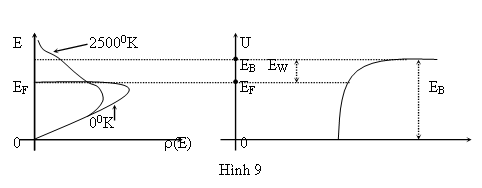
Nếu ta nung nóng khối kim loại tới nhiệt độ T=2.5000K, sẽ có một số điện tử có năng lượng lớn hơn EB, các điện tử này có thể vượt được ra ngoài kim loại. Người ta chứng minh được rằng, số điện tử vượt qua mỗi đơn vị diện tích trong một đơn vị thời gian là:
Trong đó, A0 = 6,023.1023 và K = 1,38.10-23 J/0K
Đây là phương trình Dushman-Richardson.
Người ta dùng phương trình này để đo EW vì ta có thể đo được dòng điện Jth; dòng điện này chính là dòng điện bảo hòa trong một đèn hai cực chân không có tim làm bằng kim loại muốn khảo sát.
Xét một nối C giữa hai kim loại I và II. Nếu ta dùng một Volt kế nhạy để đo hiệu điện thế giữa hai đầu của nối (A và B), ta thấy hiệu số điện thế này không triệt tiêu, theo định nghĩa, hiệu điện thế này gọi là tiếp thế. Ta giải thích tiếp thế như sau:
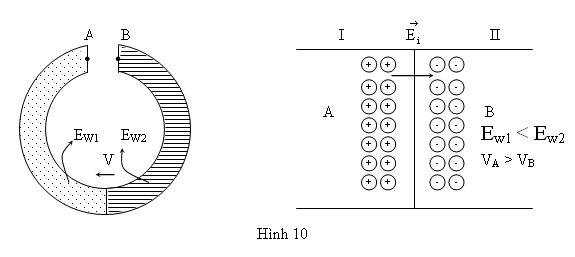
Giả sử kim loại I có công ra EW1 nhỏ hơn công ra EW2 của kim loại II. Khi ta nối hai kim loại với nhau, điện tử sẽ di chuyển từ (I) sang (II) làm cho có sự tụ tập điện tử bên (II) và có sự xuất hiện các Ion dương bên (I). Cách phân bố điện tích như trên tạo ra một điện trường Ei hướng từ (I) sang (II) làm ngăn trở sự di chuyển của điện tử. Khi Ei đủ mạnh, các điện tử không di chuyển nữa, ta có sự cân bằng nhiệt động học của hệ thống hai kim loại nối với nhau. Sự hiện hữu của điện trường Ei chứng tỏ có một hiệu điện thế giữa hai kim loại.

Notification Switch
Would you like to follow the 'Điện tử ứng dụng' conversation and receive update notifications?