| << Chapter < Page | Chapter >> Page > |
Activity 1:
| To recognise and represent multiples in order to be able to describe, compare and represent them [LO 1.3] |
| To investigate numeric patterns [LO 2.1] |
| To describe numeric patterns in your own words [LO 2.2] |
| To find output numbers [LO 2.3] |
1. When we count in 6’s we are saying the multiples of 6.
1.1 Work with a friend. One of you must count in 6’s from 0 to 102. The other one must use a calculator to check you and stop you if you make a mistake. If that happens the one with the calculator must just say, ”Stop!” and show the calculator. The counting goes on from there. Then swap over.
1.2 Now fill in the missing multiples of 6 in the table below:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| × 6 | 6 | 12 | 18 | 24 | 30 | 60 | 66 |
1.3 Now count backwards in 6’s from 102 to 0. Let a friend check you. Then swap over. Do you notice anything? Yes, multiples of 6 are all even numbers.
1.4 What patterns do you notice? Yes, the last digits seem to be 6;..2; ..8; ..4; ..0. They are repeated and so form a pattern.
Now that you are aware of this, you can count in 6’s for ever (if you concentrate)!
1.5 Count in 6’s and complete the flow diagram:
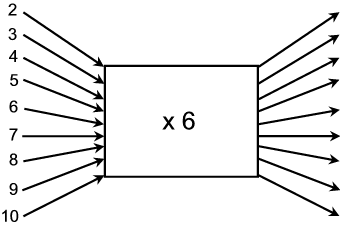
1.6 How do we programme the calculator to count in 6’s?
Press clear and
1.7 Write down the multiples of 6 from 102 to 0:
1.8 How do we programme the calculator to count backwards in 6’s from 102?
Press clear and
Now you can really count in 6’s easily, so let’s move on to 7’s.
2. Multiples of 7
2.1 Now use your calculator (if necessary) to count in 7’s and complete the flow diagram:
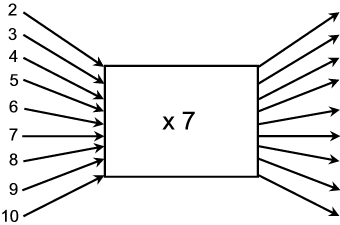
Can you spot any patterns? Two are written below. Try to spot some more and discuss with a friend.
2.2 Now fill in the missing multiples of 7:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| × 7 | 7 | 14 | 21 | 70 | 77 |
There seems to be some sort of repetition after the first 9 multiples. Does it continue?
Are there any other patterns? Write down what you have noticed.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| × 6 | 6 | 12 | 18 | 24 | ||||||||
| × 7 | 7 | 14 | 21 | 28 |
2.5 Now compare the two rows (across) of answers. A very interesting pattern appears to be emerging.
Look: 1 × 7 = 1× 6 + 1
5 × 7 = 5 × 6 + ……
9 × 7 = 9 × 6 + ……
2 × 7 = 2 × 6 + …….
6 × 7 = 6 × 6 + ……
10 × 7 = 10 × 6 + …..
4 × 7 = 4 × 6 + ……
8 × 7 = 8 × 6 + ……
12 × 7 = 12 × 6 +……
3. Multiples of 8
3.1 The numbers jump in 8 wholes. Use the calculator to count in 8’s and write down the missing multiples of 8.
0, 8, 16, 24, 32,……., ……., …………, ………, ………….,…………,………., …………, ……., …….., …………, ……… .
3.2 Another way of saying: 8 + 8 + 8 + 8 is 4 × 8.
Now complete the flow diagram:
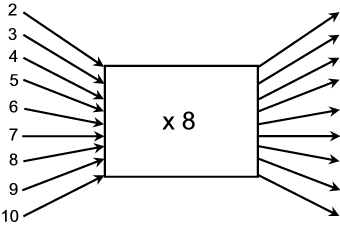
3.3 Spot a pattern. Write down the missing multiples of 8 in the table below and look at the last digit of each one.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| × 8 | 8 | 16 | 80 | 88 |
Look carefully:
8 ; 1 6 ; 2 4 ; 3 2 ; 4 0 ; 48; 56; 64; 72; 80; 88; 96

Notification Switch
Would you like to follow the 'Mathematics grade 4' conversation and receive update notifications?