1. Home
  2. Physics 105: adventures in
  3. W3- normal forces and ramps
  4. Normal, tension, and other

Normal, tension, and other examples of forces  (Page 3/10)

<< Chapter < Page
  Physics 105: adventures in     Page 3 / 10
Chapter >> Page >

F net ∥ = w ∥ − f size 12{F rSub { size 8{"net " \lline \lline } } =w rSub { size 8{ \lline \lline } } - f} {} ,

and substituting this into Newton’s second law, a ∥ = F net ∥ m size 12{a rSub { size 8{ \lline \lline } } = { {F rSub { size 8{"net " \lline \lline } } } over {m} } } {} , gives

a ∥ = F net ∣ ∣ m = w ∥ − f m = mg sin ( 25º ) − f m size 12{a rSub { size 8{ \lline \lline } } = { {F rSub { size 8{"net " \lline \lline } } } over {m} } = { {w rSub { size 8{ \lline \lline } } - f} over {m} } = { { ital "mg""sin" \( "25"° \) - f} over {m} } } {} .

We substitute known values to obtain

a ∥ = ( 60 . 0 kg ) ( 9 . 80 m/s 2 ) ( 0 . 4226 ) − 45 . 0 N 60 . 0 kg size 12{a rSub { size 8{ \lline \lline } } = { { \( "60" "." "0 kg" \) \( 9 "." "80 m/s" rSup { size 8{2} } \) \( 0 "." "4226" \) - "45" "." "0 N"} over {"60" "." "0 kg"} } } {} ,

which yields

a ∥ = 3 . 39 m/s 2 size 12{a rSub { size 8{ \lline \lline } } =3 "." "39 m/s" rSup { size 8{2} } } {} ,

which is the acceleration parallel to the incline when there is 45.0 N of opposing friction.

Discussion

Since friction always opposes motion between surfaces, the acceleration is smaller when there is friction than when there is none. In fact, it is a general result that if friction on an incline is negligible, then the acceleration down the incline is a = g sin θ size 12{a=g"sin"θ} {} , regardless of mass . This is related to the previously discussed fact that all objects fall with the same acceleration in the absence of air resistance. Similarly, all objects, regardless of mass, slide down a frictionless incline with the same acceleration (if the angle is the same).

Resolving weight into components

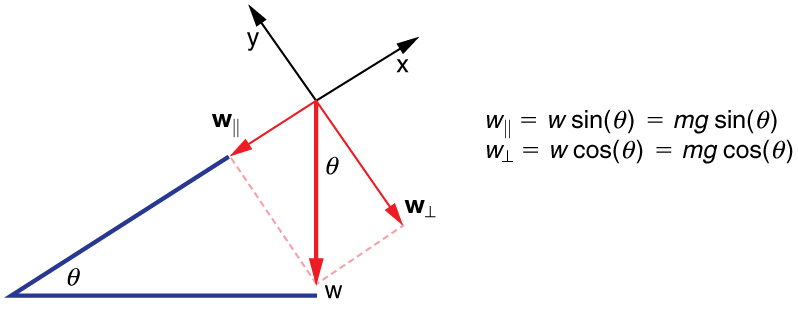
Vector arrow W for weight is acting downward. It is resolved into components that are parallel and perpendicular to a surface that has a slope at angle theta to the horizontal. The coordinate direction x is labeled parallel to the sloped surface, with positive x pointing uphill. The coordinate direction y is labeled perpendicular to the sloped surface, with positive y pointing up from the surface. The components of w are w parallel, represented by an arrow pointing downhill along the sloped surface, and w perpendicular, represented by an arrow pointing into the sloped surface. W parallel is equal to w sine theta, which is equal to m g sine theta. W perpendicular is equal to w cosine theta, which is equal to m g cosine theta.
An object rests on an incline that makes an angle θ with the horizontal.

When an object rests on an incline that makes an angle θ size 12{θ} {} with the horizontal, the force of gravity acting on the object is divided into two components: a force acting perpendicular to the plane, w ⊥ size 12{w rSub { size 8{ ortho } } } {} , and a force acting parallel to the plane, w ∥ size 12{w rSub { size 8{ \lline \lline } } } {} . The perpendicular force of weight, w ⊥ size 12{w rSub { size 8{ ortho } } } {} , is typically equal in magnitude and opposite in direction to the normal force, N size 12{N} {} . The force acting parallel to the plane, w ∥ size 12{w rSub { size 8{ \lline \lline } } } {} , causes the object to accelerate down the incline. The force of friction, f size 12{f} {} , opposes the motion of the object, so it acts upward along the plane.

It is important to be careful when resolving the weight of the object into components. If the angle of the incline is at an angle θ size 12{θ} {} to the horizontal, then the magnitudes of the weight components are

w ∥ = w sin ( θ ) = mg sin ( θ ) size 12{w rSub { size 8{ \lline \lline } } =w"sin" \( θ \) = ital "mg""sin" \( θ \) " "} {}

and

w ⊥ = w cos ( θ ) = mg cos ( θ ) size 12{w rSub { size 8{ ortho } } =w"cos" \( θ \) = ital "mg""cos" \( θ \) } {} .

Instead of memorizing these equations, it is helpful to be able to determine them from reason. To do this, draw the right triangle formed by the three weight vectors. Notice that the angle θ size 12{θ} {} of the incline is the same as the angle formed between w size 12{w} {} and w ⊥ size 12{w rSub { size 8{ ortho } } } {} . Knowing this property, you can use trigonometry to determine the magnitude of the weight components:

cos ( θ ) = w ⊥ w w ⊥ = w cos ( θ ) = mg cos ( θ ) alignl { stack { size 12{"cos" \( θ \) = { {w rSub { size 8{ ortho } } } over {w} } } {} #w rSub { size 8{ ortho } } =w"cos" \( θ \) = ital "mg""cos" \( θ \) {} } } {}

sin ( θ ) = w ∥ w w ∥ = w sin ( θ ) = mg sin ( θ ) alignl { stack { size 12{"sin" \( θ \) = { {w rSub { size 8{ \lline \lline } } } over {w} } } {} #w rSub { size 8{ \lline \lline } } =w"sin" \( θ \) = ital "mg""sin" \( θ \) {} } } {}

Take-home experiment: force parallel

To investigate how a force parallel to an inclined plane changes, find a rubber band, some objects to hang from the end of the rubber band, and a board you can position at different angles. How much does the rubber band stretch when you hang the object from the end of the board? Now place the board at an angle so that the object slides off when placed on the board. How much does the rubber band extend if it is lined up parallel to the board and used to hold the object stationary on the board? Try two more angles. What does this show?

Tension

A tension     is a force along the length of a medium, especially a force carried by a flexible medium, such as a rope or cable. The word “tension ” comes from a Latin word meaning “to stretch.” Not coincidentally, the flexible cords that carry muscle forces to other parts of the body are called tendons . Any flexible connector, such as a string, rope, chain, wire, or cable, can exert pulls only parallel to its length; thus, a force carried by a flexible connector is a tension with direction parallel to the connector. It is important to understand that tension is a pull in a connector. In contrast, consider the phrase: “You can’t push a rope.” The tension force pulls outward along the two ends of a rope.
<< Chapter < Page Page > Chapter >>
Practice Key Terms 3

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Physics 105: adventures in physics. OpenStax CNX. Dec 02, 2015 Download for free at http://legacy.cnx.org/content/col11916/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Physics 105: adventures in physics' conversation and receive update notifications?

Ask