| << Chapter < Page | Chapter >> Page > |
The discussion here will focus on the relationship between ratio, frequency, and musical intervals. The interval between two pitches depends on the ratio of their frequencies . There are simple, ideal ratios as expressed in a harmonic series , and then there is the more complex reality of equal temperament , in which the frequency ratios are not so simple and are best written as roots or decimals. Here is one more exercise before we go on to discussions of music.
The kind of sound waves that music is made of are a lot like the adult and child walking along steadily in the example above . Low notes have long wavelengths, like the long stride of an adult. Their frequencies, like the frequency of the adult's steps, are low. High notes have shorter wavelengths, like the small stride of the child. Their frequencies, like the frequency of a child's steps, are higher. (See Sound, Physics and Music for more on this.)
It is easy to spot simple frequency relationships, like 2:1, but what about more complicated ratios? Remember that you are saying the ratio of one frequency to another IS (equals) another ratio(or fraction or decimal) . This idea can be written as a simple mathematical expression. With enough information and a little bit of algebra, you can solve this equation for any number that you don't have.
If you remember enough algebra, you'll notice that the units for frequency in this equation must be the same: if frequency #1 is in hertz, frequency #2 must be in hertz also. In all the examples and problems below, I am going to assume all frequencies are in hertz (waves per second), but you can use any frequency unit as long as they are both the same . Most musicians don't talk about frequency much, and when they do, they rarely mention units, but just say, for example, "A 440".

Say you would like to compare the frequencies of two sounds. Sound #1 is 630 and sound #2 is 840. If you use the expression given above and do the division on a calculator, the answer will be a decimal. If you simply reduce the fraction to lowest terms, or if you know the fraction that these decimals represent, you can see that you have a simple ratio of 3:4. Notice that if you switch the frequencies in the expression, the ratio also switches from 3:4 to 4:3. So it doesn't really matter which frequency you put on top; you will get the right answer as long as you keep track of which frequency is which.
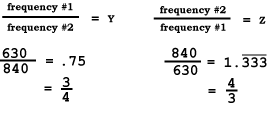

Notification Switch
Would you like to follow the 'Sound, physics and music' conversation and receive update notifications?