Measurement  (Page 3/3)

When the length of one of the sides is multiplied by a constant the effect is to multiply the original volume by that constant, as for the example in [link] .

Right pyramids, right cones and spheres

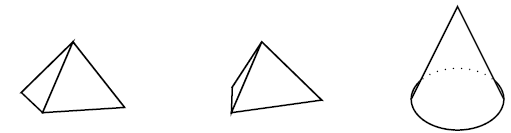
A pyramid is a geometric solid that has a polygon base and the base is joined to a point, called the apex. Two examples of pyramids are shown in the left-most and centre figures in [link] . The right-most figure has an apex which is joined to a circular base and this type of geometric solid is called a cone. Cones are similar to pyramids except that their bases are circles instead of polygons.

Surface Area of a Pyramid

The surface area of a pyramid is calculated by adding the area of each face together.

Volume of a Pyramid: The volume of a pyramid is found by:

where $A$ is the area of the base and $h$ is the height.

A cone is like a pyramid, so the volume of a cone is given by:

A square pyramid has volume

where $a$ is the side length of the square base.

What is the volume of a square pyramid, 3cm high with a side length of 2cm?

1. Determine the correct formula

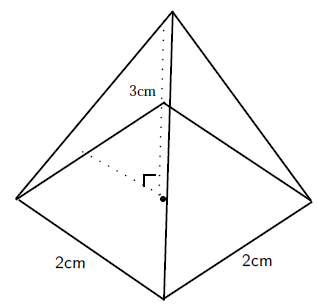
   The volume of a pyramid is

   $$V=\frac{1}{3}A·h,$$

   where $A$ is the area of the base and $h$ is the height of the pyramid. For a square base this means

   $$V=\frac{1}{3}a·a·h$$

   where $a$ is the length of the side of the square base.

2. Substitute the given values
   $$\begin{array}{ccc}& =& \frac{1}{3}·2·2·3\hfill \\ & =& \frac{1}{3}·12\hfill \\ & =& 4c{m}^3\hfill \end{array}$$

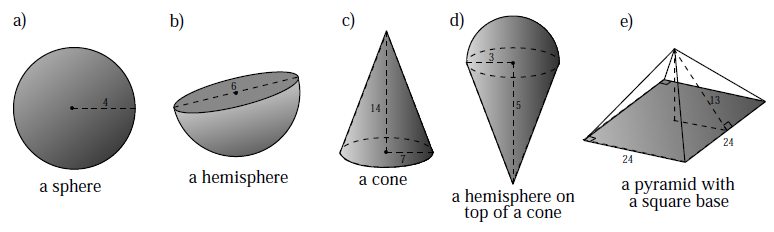
We accept the following formulae for volume and surface area of a sphere (ball).

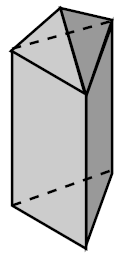
A triangular pyramid is placed on top of a triangular prism. The prism has an equilateral triangle of side length 20 cm as a base, and has a height of 42 cm. The pyramid has a height of 12 cm.

1. Find the total volume of the object.
2. Find the area of each face of the pyramid.
3. Find the total surface area of the object.

1. Find the volume of the triangular prism We use the formula for the volume of a triangular prism:
   $\begin{array}{ccc}V& =& \frac{1}{2}b{h}^2\hfill \\ & =& \frac{1}{2}20{42}^2\hfill \\ & =& 17640\hfill \end{array}$
2. Find the volume of the triangular pyramid We use the formula for the volume of a triangular pyramid:
   $\begin{array}{ccc}V& =& \frac{1}{6}b{h}^2\hfill \\ & =& \frac{1}{6}20{42}^2\hfill \\ & =& 5880\hfill \end{array}$
3. Find the volume We note that we can simply add the volumes of each of the two shapes. So we obtain: $17640+5880=23520$ . This is the answer to part a.
4. Find the area of the faces of the pyramid We note that we have four triangles that make up the pyramid. So the area of each face is simply:
   $\begin{array}{ccc}\mathrm{Area}& =& \frac{1}{2}bh\hfill \\ & =& \frac{1}{2}2042\hfill \\ & =& 420\hfill \end{array}$
   This is the answer to part b.
5. Find the area of the pyramid The total area of the pyramid is simply $4\times 420=1680$
6. Find the area of the prism The surface area of the prism is:
   $\begin{array}{ccc}\mathrm{Surface\; area}& =& b\times h+2\times H\times S+H\times b\hfill \\ & =& \mathrm{20}\times \mathrm{20}+2\times \mathrm{12}\times \mathrm{20}+\mathrm{12}\times \mathrm{20}\hfill \\ & =& 1120\hfill \end{array}$
7. Find the total surface area To find the total surface area, we must subtract the area of one face of the pyramid from the area of the prism. We must also subtract the area of one of the triangular faces of the prism. Doing this gives the total surface area as: $1120-420+1680-420=1960$ This is the answer to part c.

Surface area and volume

1. Calculate the volumes and surface areas of the following solids: *Hint for (e): find the perpendicular height using Pythagoras.

   

2. Water covers approximately 71% of the Earth's surface. Taking the radius of the Earth to be 6378 km, what is the total area of land (area not covered by water)?