Поим за извод и негово толкување  (Page 2/2)

Диференцијабилност во точка и интевал

Постоењето на извод во дадена точка означува дека функцијата е диференцијабилна во таа точка. За функција која нема извод во дадена точка се вели дека не е диференцијабилна во точката.

Ако функција е диференцијабилна во секоја точка од даден интервал, за функцијата се вели дека е диференцијабилна на интервалот.

Изводот на функција може да има различни толкувања во зависност од видот на проблемот што се разгледува. Ќе наведеме неколку толкувања на изводот во различни области.

Геометриско толкување на изводот

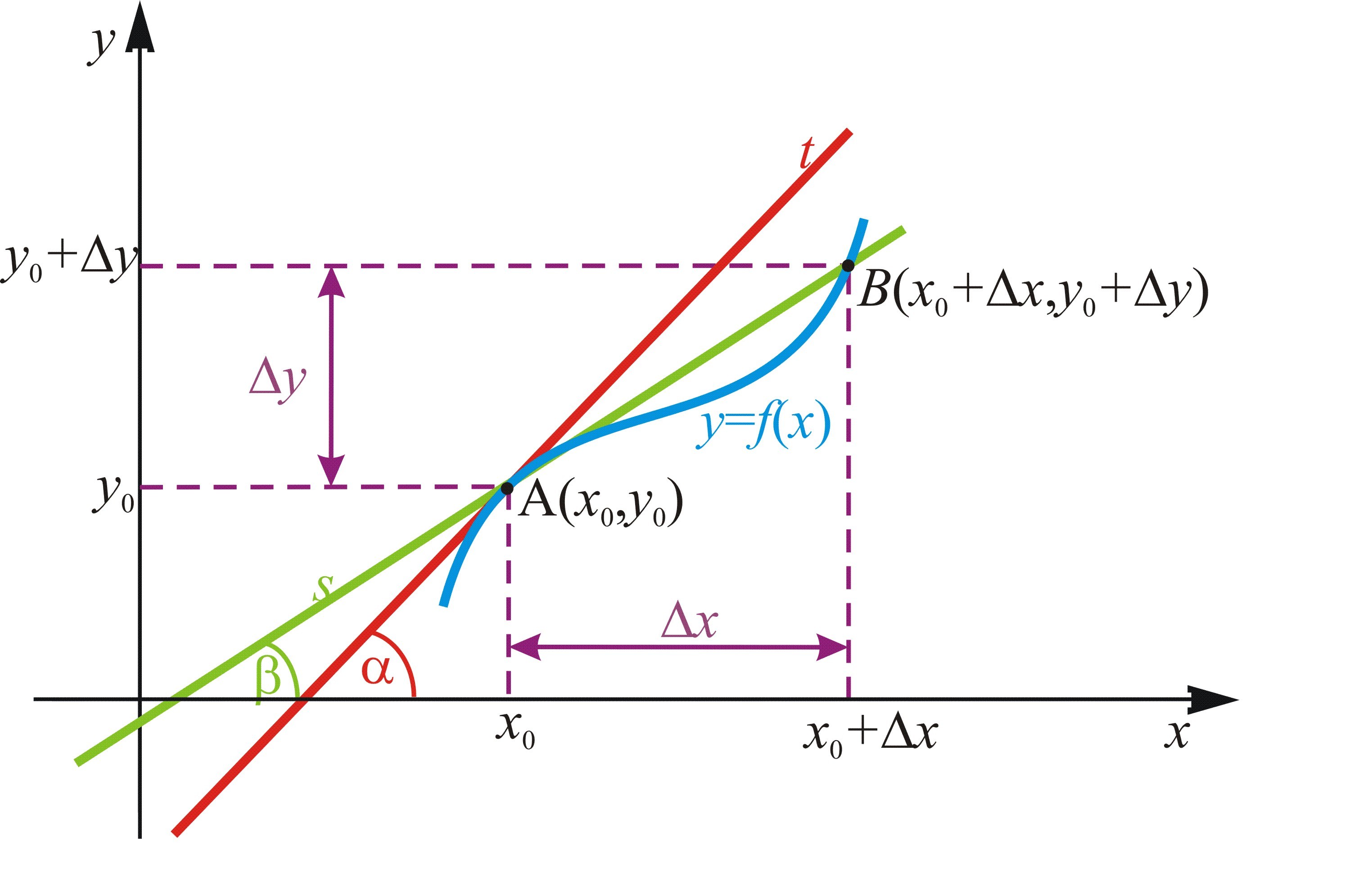
Нека функцијата $y=f(x)$ се разледува во координатен ситем $\text{xOy}$ во кој таа е претставена со нејзиниот график. На кривата се разгледуваат две блиски точки $A(x_0,f(x_0))$ и $B(x_0+\mathrm{\Delta x},f(x_0+\mathrm{\Delta x}))$ . Правата која ги сврзува овие точки се нарекува секанта и на Слика 1 е означена со $s$ . Кога точката $B$ се движи по кривата кон точката $A$ , тогаш $\mathrm{\Delta x}\to 0$ и $\mathrm{\Delta y}\to 0$ . Во граничен случај секантата ќе премине во тангента $t$ на кривата во точката $A$ .

Дефиниција.

Граничната вредност

$\underset{\mathrm{\Delta x}\to 0}{\text{lim}}\frac{f(x_0+\mathrm{\Delta x})-f(x_0)}{\mathrm{\Delta x}}=\underset{\mathrm{\Delta x}\to 0}{\text{lim}}\text{tg}\beta =\text{tg}\alpha$ ,

е изводот $f^{\text{'}}(x_0)$ и тој е еднаков со коефициент на правецот на тангентата на кривата $y=f(x)$ во точката $A(x_0,f(x_0))$ , односно изводот е тангенс од аголот што тангентата на кривата во дадената точка го зафаќа со позитивната насока на $x-$ оската (Слика 1).

Ова значи дека коефициентот на правецот на тангентата $k$ во точката $x_0$ е

$k=f^{\text{'}}(x_0)=\text{tg}\alpha \text{.}$

Кинематичко толкување на изводот

Нека М е материјална точка која се движи по одредена патека. Ако движењето е рамномерно и ако за време $t$ таа изминува пат $s$ , количникот $\frac{s}{t}$ ја претставува брзината на движење на материјалната точка. Ако пак движењето е нерамномерно, во различен момент материјалната точка се движи со различна брзина. Нека се разгледува движењето на точката М во момент $t_0$ . За време $\mathrm{\Delta t}$ материјалната точка ќе измине пат $s(t_0+\mathrm{\Delta t})-s(t_0),$ а количникот

се нарекува средна брзина на движење на материјалната точка М во моментот $t_0$ .

Дефиниција.

Граничната вредност

е брзина на движење на материјалната точка М во моментот $t_0$ .

Бидејќи и брзината е променлив процес, нејзиниот извод ја изразува промената на брзината која се нарекува забрзување. Поимот за брзина не се врзува само со движење на материјална точка, туку тој ја означува брзината со која се менува било кој променлив процес.

Концентрација на раствор - едно толкување на изводот во хемијата

Нека е даден сад со определено количество вода и нека во садот се стави некое количество сол. После некое време солта ќе се раствори и водата во садот ќе стане солена. Ако волуменот на водата во садот е $V$ , а количеството на растворена сол е $Q$ , јасно е дека

$Q=f(V)$ .

Нека со $\mathrm{\Delta V}$ се означи мала (единечна) промена на волуменот на водата а со $\mathrm{\Delta Q}$ се означи промената на количеството растворена сол.

Количникот

претставува количество растворена сол во единечен (мал) волумен $\mathrm{\Delta V}$ и се нарекува средна концентрација на растворот во волуменот $\mathrm{\Delta V}$ .

Дефиниција.

Граничната вредност

се нарекува концентрација на растворот во определен волумен.

Ова значи дека изводот на количеството растворена сол по волуменот на вода во која се раствора е концентрација на растворот.

Забелешка.

Поимот за извод на функција воведен преку преминување на секантата во тангента на кривата (геометриско толкување на изводот) е воведен од Лајбниц (1646-1716), а независно од него Њутн (1642-1727) го вовел изводот како брзина на движење (кинематичко толкување), па затоа заедно и Лајбниц и Њутн се сметаат за творци на диференцијалното сметање.