| << Chapter < Page | Chapter >> Page > |
- Using all the different kinds of trapezium as a guide, write down in words how you will recognise the shape.
1.6 On the shape sheet you will find two kinds of KITE. Cut out both kinds and find any lines of symmetry.
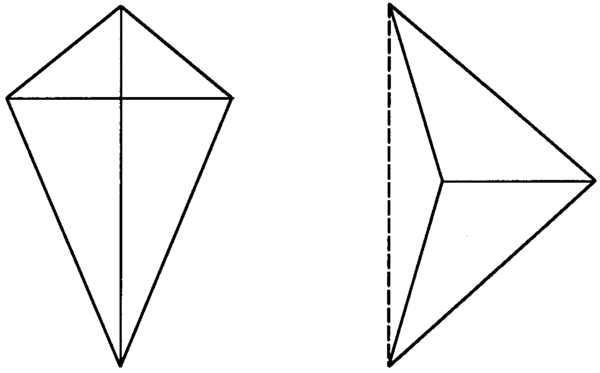
A kite is a kind of bird; it is also the name of the toy that can be made to fly in the wind, tethered by a string that is used to manipulate it. Modern kites have different ingenious shapes, but the quadrilateral gets its name from the simple paper kites, which are easy to make using two thin sticks of different lengths, some paper, glue and string – and a tail for a stabilizer.
Is there a special name for the dotted line in one of the kites above?
2. Side lengths
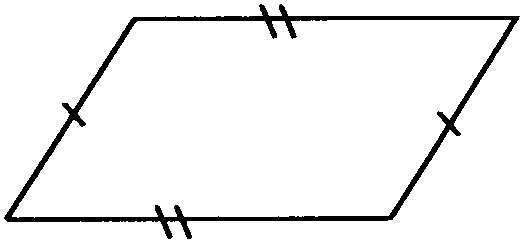
Study the examples of the six types of quadrilateral. First measure the sides of each as accurately as you can, to see whether any of the sides are the same length, and mark them. In this sketch of a parallelogram, the opposite sides have been marked with little lines to show which sides have equal lengths.
- Is a rhombus just a parallelogram with all four sides equal?
3. Parallel sides
Parallel lines (as you know) are lines that always stay equally far from each other. This means that they will never meet, no matter how far you extend them. They need not be the same length. You already know how to mark parallel lines with little arrows to show which are parallel.
Now study your quadrilaterals again to see whether you can identify the parallel lines with a bit of measuring. This is not easy, but you will do well if you concentrate and work methodically.
- If you could change just one side of any trapezium, could you turn it into a parallelogram? What would you have to change?
4. Internal angle sizes
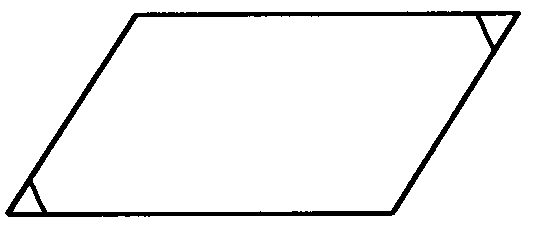
It is easy to measure the internal angles with your protractor. Write the sizes in on the sketch, and then see whether you find right angles or equal angles. You can mark equal angles with lines to show which are which, as in this sketch of the parallelogram.
- Add up all the internal angles of every quadrilateral you measured and write the answer next to the quadrilateral. Does the answer surprise you?
5. Diagonals
Diagonals run from one internal vertex to the opposite vertex. Draw the diagonals in all the quadrilaterals (sometimes they will be on top of the lines of symmetry).
Measure the lengths of the diagonals to identify those quadrilaterals where the two diagonals are the same length. Mark them if they are the same, just as you marked the equal sides.
Use your protractor to carefully measure the two angles that the diagonals make where they cross (intersect). Take note of those quadrilaterals where the diagonals cross at right angles.
The diagonals also divide the internal angles of the quadrilateral. Measure these angles and make a note of those cases where the internal angle is bisected (halved) by the diagonal.
6. Tabulate your results
Complete the following table to summarise your results for all the characteristics of all the quadrilaterals.
Think very carefully about whether what you have observed is true for all versions of the same shape. For example, you may find that the two diagonals of a certain trapezium are equal; but would they be equal for all trapeziums? And if a kite has two equal diagonals, is it correct to call it a kite?
This table contains very useful information. Make sure your table is correct, and keep it for the following exercises.
| Square | Rhombus | Parallelo-gram | Rectangle | Trapezium | Kite | ||
| Number of lines of symmetry | |||||||
| All sides equal | |||||||
| 2 pairs of opposite sides equal | |||||||
| 2 pairs of adjacent sides equal | |||||||
| 2 pairs of parallel sides | |||||||
| Only 1 pair of parallel sides | |||||||
| No parallel sides | |||||||
| All internal angles equal | |||||||
| 2 pairs of opposite internal angles equal | |||||||
| Only 1 pair of opposite angles equal | |||||||
| Diagonals always equal | |||||||
| Diagonals are perpendicular | |||||||
| Both diagonals bisect internal angles | |||||||
| Only one diagonal bisects internal angles | |||||||
| Both diagonals bisect area | |||||||
| Only one diagonal bisects area | |||||||
| Diagonals bisect each other | |||||||
Assessment
| LO 3 |
| Space and Shape (Geometry)The learner will be able to describe and represent characteristics and relationships between two-dimensional shapes and three–dimensional objects in a variety of orientations and positions. |
| We know this when the learner: |
| 3.2 in contexts that include those that may be used to build awareness of social, cultural and environmental issues, describes the interrelationships of the properties of geometric figures and solids with justification, including: |
| 3.2.2 transformations. |
| 3.3 uses geometry of straight lines and triangles to solve problems and to justify relationships in geometric figures; |
| 3.4 draws and/or constructs geometric figures and makes models of solids in order to investigate and compare their properties and model situations in the environment. |

Notification Switch
Would you like to follow the 'Mathematics grade 9' conversation and receive update notifications?