Electric potential energy: potential difference  (Page 12/10)

When a free positive charge $q$ is accelerated by an electric field, such as shown in [link] , it is given kinetic energy. The process is analogous to an object being accelerated by a gravitational field. It is as if the charge is going down an electrical hill where its electric potential energy is converted to kinetic energy. Let us explore the work done on a charge $q$ by the electric field in this process, so that we may develop a definition of electric potential energy.

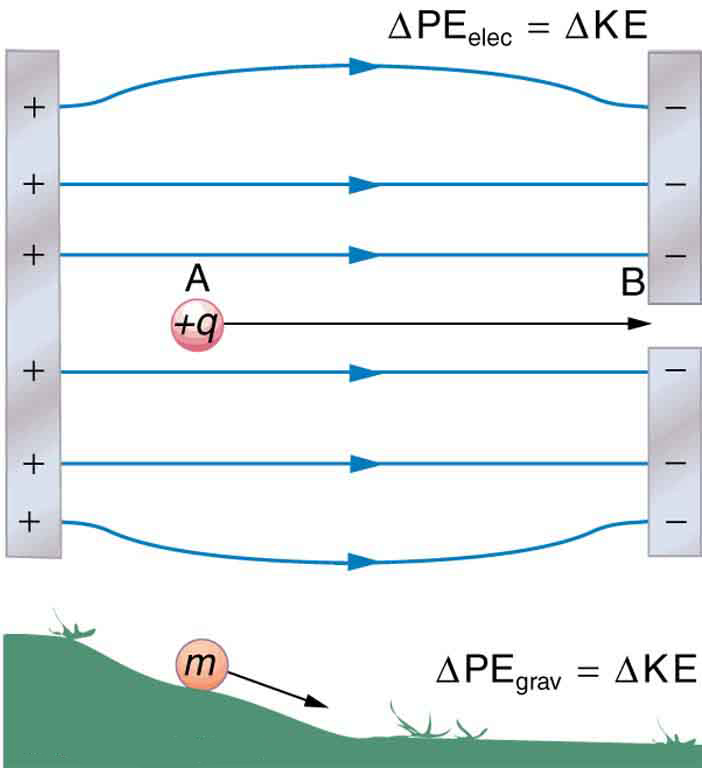
The electrostatic or Coulomb force is conservative, which means that the work done on $q$ is independent of the path taken. This is exactly analogous to the gravitational force in the absence of dissipative forces such as friction. When a force is conservative, it is possible to define a potential energy associated with the force, and it is usually easier to deal with the potential energy (because it depends only on position) than to calculate the work directly.

We use the letters PE to denote electric potential energy, which has units of joules (J). The change in potential energy, $\text{Δ}\text{PE}$ , is crucial, since the work done by a conservative force is the negative of the change in potential energy; that is, $W=\text{–Δ}\text{PE}$ . For example, work $W$ done to accelerate a positive charge from rest is positive and results from a loss in PE, or a negative $\text{Δ}\text{PE}$ . There must be a minus sign in front of $\text{Δ}\text{PE}$ to make $W$ positive. PE can be found at any point by taking one point as a reference and calculating the work needed to move a charge to the other point.

Gravitational potential energy and electric potential energy are quite analogous. Potential energy accounts for work done by a conservative force and gives added insight regarding energy and energy transformation without the necessity of dealing with the force directly. It is much more common, for example, to use the concept of voltage (related to electric potential energy) than to deal with the Coulomb force directly.

Calculating the work directly is generally difficult, since $W=\text{Fd}\text{cos}\theta$ and the direction and magnitude of $F$ can be complex for multiple charges, for odd-shaped objects, and along arbitrary paths. But we do know that, since $F=\text{qE}$ , the work, and hence $\text{ΔPE}$ , is proportional to the test charge $\mathrm{q.}$ To have a physical quantity that is independent of test charge, we define electric potential     $V$ (or simply potential, since electric is understood) to be the potential energy per unit charge: