Decimals: reading and writing decimals

Section overview

• Digits to the Right of the Ones Position
• Decimal Fractions
• Reading Decimal Fractions
• Writing Decimal Fractions

Digits to the right of the ones position

We began our study of arithmetic ( [link] ) by noting that our number system is called a positional number system with base ten. We also noted that each position has a particular value. We observed that each position has ten times the value of the position to its right.

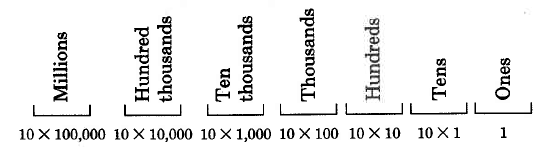
This means that each position has $\frac{1}{10}$ the value of the position to its left.

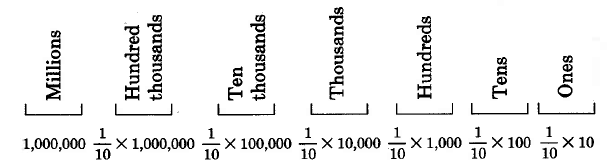
Thus, a digit written to the right of the units position must have a value of $\frac{1}{\text{10}}$ of 1. Recalling that the word "of" translates to multiplication $\left(\cdot \right)$ , we can see that the value of the first position to the right of the units digit is $\frac{1}{\text{10}}$ of 1, or

$\frac{1}{\text{10}}\cdot 1=\frac{1}{\text{10}}$

The value of the second position to the right of the units digit is $\frac{1}{\text{10}}$ of $\frac{1}{\text{10}}$ , or

$\frac{1}{\text{10}}\cdot \frac{1}{\text{10}}=\frac{1}{{\text{10}}^2}=\frac{1}{\text{100}}$

The value of the third position to the right of the units digit is $\frac{1}{\text{10}}$ of $\frac{1}{\text{100}}$ , or

$\frac{1}{\text{10}}\cdot \frac{1}{\text{100}}=\frac{1}{{\text{10}}^3}=\frac{1}{\text{1000}}$

This pattern continues.

We can now see that if we were to write digits in positions to the right of the units positions, those positions have values that are fractions. Not only do the positions have fractional values, but the fractional values are all powers of 10 $\left(\text{10},{\text{10}}^2,{\text{10}}^3,\dots \right)$ .

Decimal fractions

Decimal point, decimal

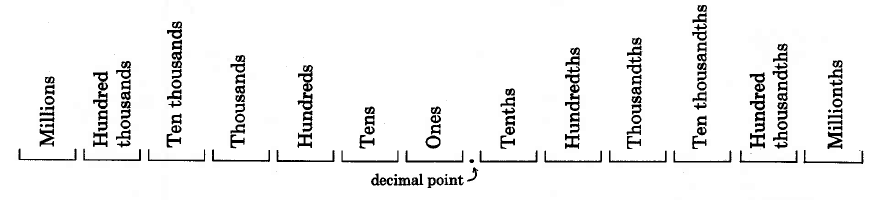
Notice that decimal numbers have the suffix "th."

Decimal fraction

The following numbers are examples of decimals.

1. 42.6
   

   The 6 is in the tenths position.

   $\text{42}\text{.}6=\text{42}\frac{6}{\text{10}}$

2. 9.8014
   

   The 8 is in the tenths position.
   The 0 is in the hundredths position.
   The 1 is in the thousandths position.
   The 4 is in the ten thousandths position.

   $9\text{.}\text{8014}=9\frac{\text{8014}}{\text{10},\text{000}}$

3. 0.93
   

   The 9 is in the tenths position.
   The 3 is in the hundredths position.

   $0\text{.}\text{93}=\frac{\text{93}}{\text{100}}$

   Quite often a zero is inserted in front of a decimal point (in the units position) of a decimal fraction that has a value less than one. This zero helps keep us from overlooking the decimal point.
4. 0.7
   

   The 7 is in the tenths position.

   $0\text{.}7=\frac{7}{\text{10}}$

   We can insert zeros to the right of the right-most digit in a decimal fraction without changing the value of the number.
   $\frac{7}{\text{10}}=0\text{.}7=0\text{.}\text{70}=\frac{\text{70}}{\text{100}}=\frac{7}{\text{10}}$

Reading decimal fractions

Reading a decimal fraction

1. Read the whole number part as usual. (If the whole number is less than 1, omit steps 1 and 2.)
2. Read the decimal point as the word "and."
3. Read the number to the right of the decimal point as if it were a whole number.
4. Say the name of the position of the last digit.