Complex numbers  (Page 4/2)

While the fundamental signal used in electrical engineering is the sinusoid, it can be expressed mathematically in terms of an even more fundamental signal: the complex exponential . Representing sinusoids in terms of complex exponentials is not a mathematical oddity. Fluency with complex numbers and rational functions of complex variables is a critical skill all engineers master.Understanding information and power system designs and developing new systems all hinge on using complex numbers. In short, they are critical to modern electrical engineering, a realization made over a century ago.

Definitions

The notion of the square root of $-1$ originated with the quadratic formula: the solution of certain quadratic equations mathematically exists only if the so-called imaginary quantity $\sqrt{-1}$ could be defined. Euler first used $i$ for the imaginary unit but that notation did not take hold untilroughly Ampère's time. Ampère used the symbol $i$ to denote current (intensité de current).It wasn't until the twentieth century that the importance of complex numbers to circuit theory became evident. By then, using $i$ for current was entrenched and electrical engineers chose $i$ for writing complex numbers.

An imaginary number has the form $ib=\sqrt{-b^2}$ . A complex number , $z$ , consists of the ordered pair ( $a$ , $b$ ), $a$ is the real component and $b$ is the imaginary component (the $i$ is suppressed because the imaginary component of the pair is always in the second position). The imaginary number $ib$ equals ( $0$ , $b$ ). Note that $a$ and $b$ are real-valued numbers.

[link] shows that we can locate a complex number in what we call the complex plane . Here, $a$ , the real part, is the $x$ -coordinate and $b$ , the imaginary part, is the $y$ -coordinate.

The complex plane

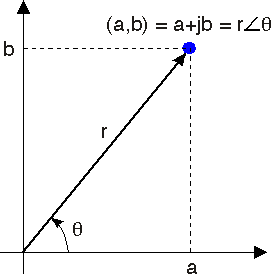
Some obvious terminology. The real part of the complex number $z=a+ib$ , written as $\Re (z)$ , equals $a$ . We consider the real part as a function that works by selecting that componentof a complex number not multiplied by $i$ . The imaginary part of $z$ , $\Im (z)$ , equals $b$ : that part of a complex number that is multiplied by $i$ . Again, both the real and imaginary parts of a complex number are real-valued.

The complex conjugate of $z$ , written as $\overline{z}$ , has the same real part as $z$ but an imaginary part of the opposite sign.

Using Cartesian notation, the following properties easily follow.

• If we add two complex numbers, the real part of the result equals the sum of the real parts and the imaginary part equals the sum of the imaginary parts. This property follows from the laws of vector addition. $$a_1+i{b}_1+a_2+i{b}_2=a_1+a_2+i(b_1+b_2)$$ In this way, the real and imaginary parts remain separate.
• The product of $i$ and a real number is an imaginary number: $ia$ . The product of $i$ and an imaginary number is a real number: $iib=-b$ because $i^2=-1$ . Consequently, multiplying a complex number by $i$ rotates the number's position by $90$ degrees.