| << Chapter < Page | Chapter >> Page > |
This brief tutorial on some key terms in linear algebra is not meant to replace or be very helpful to those of you trying togain a deep insight into linear algebra. Rather, this brief introduction to some of the terms and ideas of linear algebra ismeant to provide a little background to those trying to get a better understanding or learn about eigenvectors andeigenfunctions, which play a big role in deriving a few important ideas on Signals and Systems. The goal of theseconcepts will be to provide a background for signal decomposition and to lead up to the derivation of the Fourier Series .
A set of vectors are linearly independent if none of them can be written as a linear combination of the others.
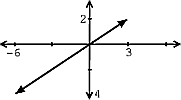
We are given the following two vectors: These are linearly independent since only if . Based on the definition, this proof shows that these vectors are indeed linearly independent. Again, wecould also graph these two vectors (see [link] ) to check for linear independence.
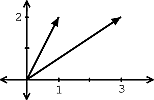
Are linearly independent?
By playing around with the vectors and doing a little trial and error, we will discover the followingrelationship: Thus we have found a linear combination of these threevectors that equals zero without setting the coefficients equal to zero. Therefore, these vectors are not linearly independent !
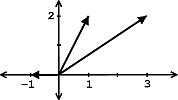
As we have seen in the two above examples, often times the independence of vectors can be easily seen through a graph.However this may not be as easy when we are given three or more vectors. Can you easily tell whether or not thesevectors are independent from [link] . Probably not, which is why the method used in the above solution becomesimportant.
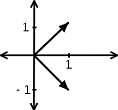
We are given the following vector where the is always in the th place and the remaining values are zero. Then the basis for is
is a basis for .
If is a basis for , then we can express any as a linear combination of the 's:
Given the following vector, writing in terms of gives us
Try and write in terms of (defined in the previous example).
In the two basis examples above, is the same vector in both cases, but we can express it in many different ways (we give only two out of many, manypossibilities). You can take this even further by extending this idea of a basis to function spaces .
Khan lecture on basis of a subspace

Notification Switch
Would you like to follow the 'Signals and systems' conversation and receive update notifications?