Acceleration  (Page 3/8)

Calculating displacement: a subway train

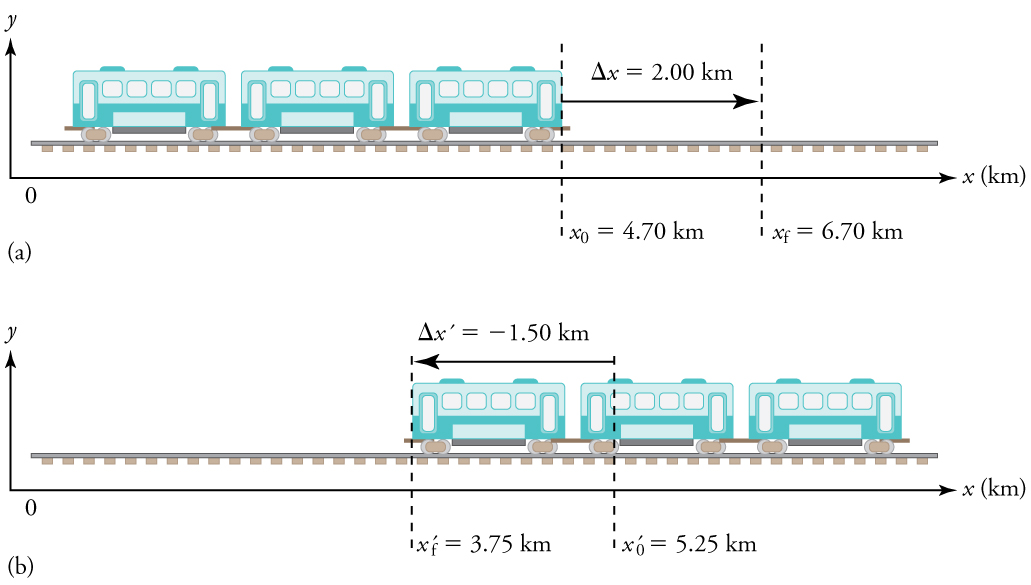
What are the magnitude and sign of displacements for the motions of the subway train shown in parts (a) and (b) of [link] ?

Strategy

A drawing with a coordinate system is already provided, so we don’t need to make a sketch, but we should analyze it to make sure we understand what it is showing. Pay particular attention to the coordinate system. To find displacement, we use the equation $\mathrm{\Delta }x=x_{\mathrm{f}}-x_0$ . This is straightforward since the initial and final positions are given.

Solution

1. Identify the knowns. In the figure we see that $x_{\mathrm{f}}=\text{6.70 km}$ and $x_0=\text{4.70 km}$ for part (a), and ${x\prime }_{\mathrm{f}}=3\text{.75 km}$ and ${x\prime }_0=5\text{.25 km}$ for part (b).

2. Solve for displacement in part (a).

3. Solve for displacement in part (b).

Discussion

The direction of the motion in (a) is to the right and therefore its displacement has a positive sign, whereas motion in (b) is to the left and thus has a negative sign.

Comparing distance traveled with displacement: a subway train

What are the distances traveled for the motions shown in parts (a) and (b) of the subway train in [link] ?

Strategy

To answer this question, think about the definitions of distance and distance traveled, and how they are related to displacement. Distance between two positions is defined to be the magnitude of displacement, which was found in [link] . Distance traveled is the total length of the path traveled between the two positions. (See Displacement .) In the case of the subway train shown in [link] , the distance traveled is the same as the distance between the initial and final positions of the train.

Solution

1. The displacement for part (a) was +2.00 km. Therefore, the distance between the initial and final positions was 2.00 km, and the distance traveled was 2.00 km.

2. The displacement for part (b) was $\text{−1.5 km.}$ Therefore, the distance between the initial and final positions was 1.50 km, and the distance traveled was 1.50 km.

Discussion

Distance is a scalar. It has magnitude but no sign to indicate direction.

Calculating acceleration: a subway train speeding up

Suppose the train in [link] (a) accelerates from rest to 30.0 km/h in the first 20.0 s of its motion. What is its average acceleration during that time interval?

Strategy

It is worth it at this point to make a simple sketch:

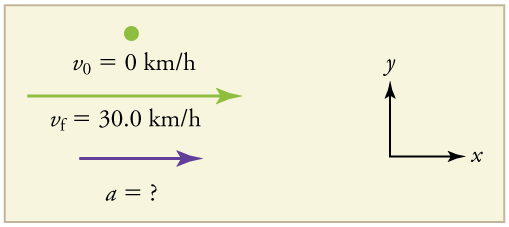
This problem involves three steps. First we must determine the change in velocity, then we must determine the change in time, and finally we use these values to calculate the acceleration.

Solution

1. Identify the knowns. $v_0=0$ (the trains starts at rest), $v_{\mathrm{f}}=\text{30}\text{.}\text{0 km/h}$ , and $\mathrm{\Delta }t=\text{20}\text{.}\text{0 s}$ .

2. Calculate $\mathrm{\Delta }v$ . Since the train starts from rest, its change in velocity is $\mathrm{\Delta }v\text{=}\text{+}\text{30.0 km/h}$ , where the plus sign means velocity to the right.

3. Plug in known values and solve for the unknown, $\stackrel{-}{a}$ .

4. Since the units are mixed (we have both hours and seconds for time), we need to convert everything into SI units of meters and seconds. (See Physical Quantities and Units for more guidance.)

Discussion

The plus sign means that acceleration is to the right. This is reasonable because the train starts from rest and ends up with a velocity to the right (also positive). So acceleration is in the same direction as the change in velocity, as is always the case.