1. Home
  2. Mechanics
  3. Rotational motion and angular
  4. Collisions of extended bodies

9.6 Collisions of extended bodies in two dimensions  (Page 3/3)

<< Chapter < Page
  Mechanics     Page 3 / 3
Chapter >> Page >

In figure a, a disk hitting a stick is compared to a tennis ball being hit by a racquet. When the ball strikes the racquet near the end with a force denoted by f ball as shown by the direction of the arrow, a backward force, f hand is exerted on the hand, In figure b, when the racquet is struck much farther down by a force F ball, a forward force, f hand is exerted on the hand as shown by the arrows. In figure (c), when the racquet is struck by the ball with a force f ball at the percussion point, no force is delivered to the hand. This implies that f hand is equal to zero.
A disk hitting a stick is compared to a tennis ball being hit by a racquet. (a) When the ball strikes the racquet near the end, a backward force is exerted on the hand. (b) When the racquet is struck much farther down, a forward force is exerted on the hand. (c) When the racquet is struck at the percussion point, no force is delivered to the hand.

Is rotational kinetic energy a vector? Justify your answer.

No, energy is always scalar whether motion is involved or not. No form of energy has a direction in space and you can see that rotational kinetic energy does not depend on the direction of motion just as linear kinetic energy is independent of the direction of motion.

Section summary

  • Angular momentum L is analogous to linear momentum and is given by L = Iω size 12{L=Iω} {} .
  • Angular momentum is changed by torque, following the relationship net τ = Δ L Δ t .
  • Angular momentum is conserved if the net torque is zero L = constant net τ = 0 or L = L ′ net τ = 0 . This equation is known as the law of conservation of angular momentum, which may be conserved in collisions.

Conceptual questions

Describe two different collisions—one in which angular momentum is conserved, and the other in which it is not. Which condition determines whether or not angular momentum is conserved in a collision?

Suppose an ice hockey puck strikes a hockey stick that lies flat on the ice and is free to move in any direction. Which quantities are likely to be conserved: angular momentum, linear momentum, or kinetic energy (assuming the puck and stick are very resilient)?

While driving his motorcycle at highway speed, a physics student notices that pulling back lightly on the right handlebar tips the cycle to the left and produces a left turn. Explain why this happens.

Problems&Exercises

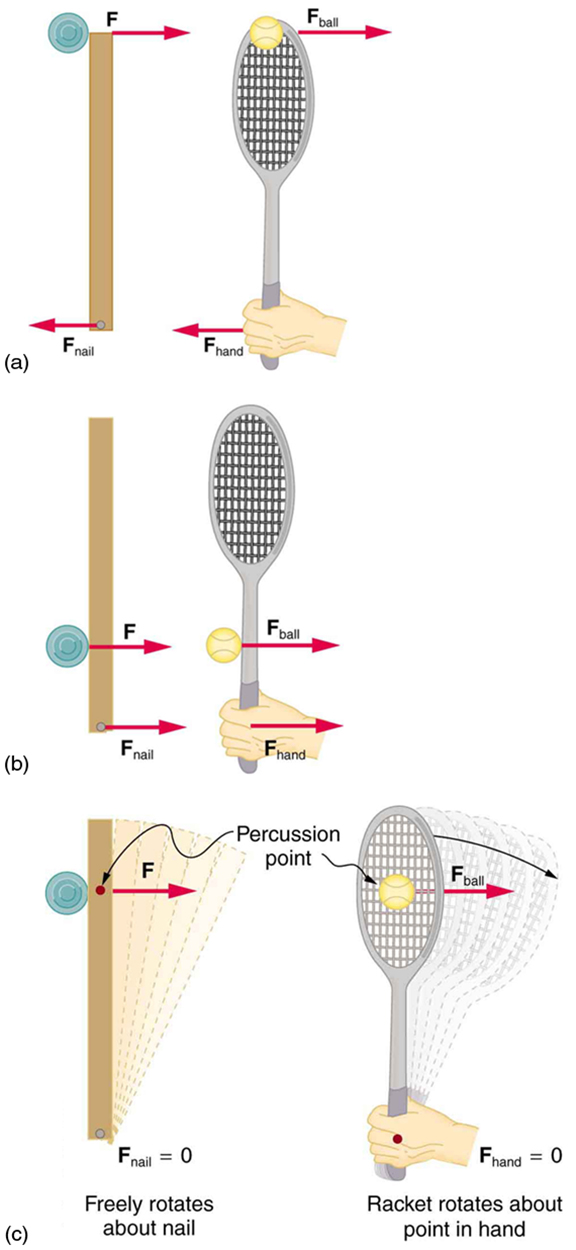
Repeat [link] in which the disk strikes and adheres to the stick 0.100 m from the nail.

(a) 0.156 rad/s

(b) 1 . 17 × 10 − 2 J size 12{1 "." "17" times "10" rSup { size 8{ - 2} } " J"} {}

(c) 0 . 188 kg ⋅ m/s size 12{0 "." "188 kg" cdot "m/s"} {}

Repeat [link] in which the disk originally spins clockwise at 1000 rpm and has a radius of 1.50 cm.

Twin skaters approach one another as shown in [link] and lock hands. (a) Calculate their final angular velocity, given each had an initial speed of 2.50 m/s relative to the ice. Each has a mass of 70.0 kg, and each has a center of mass located 0.800 m from their locked hands. You may approximate their moments of inertia to be that of point masses at this radius. (b) Compare the initial kinetic energy and final kinetic energy.

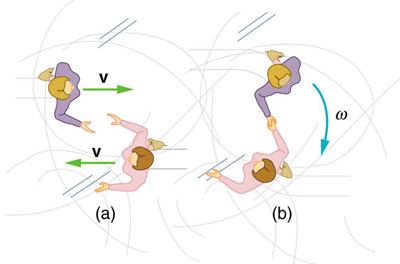
Figure a shows two skaters from the top view approaching each other from opposite directions with velocity v. In figure b two skaters then lock their right hands and start to spin in the clockwise direction with angular velocity omega.
Twin skaters approach each other with identical speeds. Then, the skaters lock hands and spin.

(a) 3.13 rad/s

(b) Initial KE = 438 J, final KE = 438 J

Suppose a 0.250-kg ball is thrown at 15.0 m/s to a motionless person standing on ice who catches it with an outstretched arm as shown in [link] .

(a) Calculate the final linear velocity of the person, given his mass is 70.0 kg.

(b) What is his angular velocity if each arm is 5.00 kg? You may treat the ball as a point mass and treat the person's arms as uniform rods (each has a length of 0.900 m) and the rest of his body as a uniform cylinder of radius 0.180 m. Neglect the effect of the ball on his center of mass so that his center of mass remains in his geometrical center.

(c) Compare the initial and final total kinetic energies.

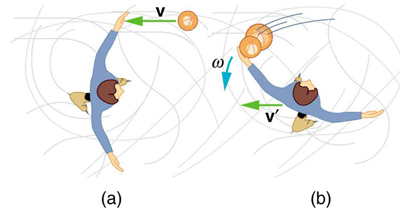
Figure a shows a skater through an overhead view with both his hands outstretched. A ball is seen approaching toward him in air with velocity v. Figure b shows that skater catching two balls in his left hand, and then, recoiling toward the left, in clockwise direction, with angular velocity omega and finally, the balls have velocity v prime.
The figure shows the overhead view of a person standing motionless on ice about to catch a ball. Both arms are outstretched. After catching the ball, the skater recoils and rotates.

Repeat [link] in which the stick is free to have translational motion as well as rotational motion.

(a) 1.70 rad/s

(b) Initial KE = 22.5 J, final KE = 2.04 J

(c) 1 . 50 kg ⋅ m/s size 12{1 "." "50 kg" cdot "m/s"} {}

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Mechanics. OpenStax CNX. Apr 15, 2013 Download for free at http://legacy.cnx.org/content/col11506/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Mechanics' conversation and receive update notifications?

Ask