9.6 Collision theory  (Page 3/11)

We can use the Arrhenius equation    to relate the activation energy and the rate constant, k , of a given reaction:

In this equation, R is the ideal gas constant, which has a value 8.314 J/mol/K, T is temperature on the Kelvin scale, E _a is the activation energy in joules per mole, e is the constant 2.7183, and A is a constant called the frequency factor , which is related to the frequency of collisions and the orientation of the reacting molecules.

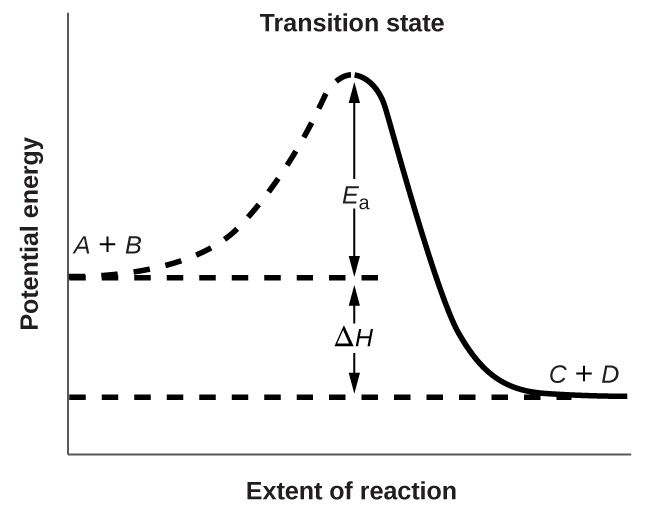
Both postulates of the collision theory of reaction rates are accommodated in the Arrhenius equation. The frequency factor A is related to the rate at which collisions having the correct orientation occur. The exponential term, $e^{\text{−}{E}_{\text{a}}\text{/}RT},$ is related to the fraction of collisions providing adequate energy to overcome the activation barrier of the reaction.

At one extreme, the system does not contain enough energy for collisions to overcome the activation barrier. In such cases, no reaction occurs. At the other extreme, the system has so much energy that every collision with the correct orientation can overcome the activation barrier, causing the reaction to proceed. In such cases, the reaction is nearly instantaneous.

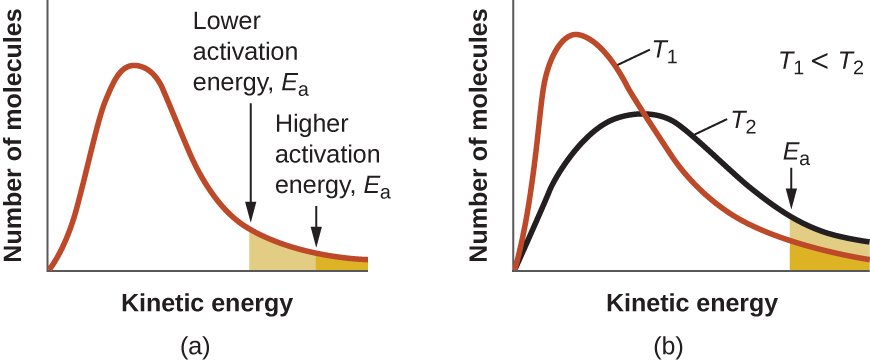
The Arrhenius equation describes quantitatively much of what we have already discussed about reaction rates. For two reactions at the same temperature, the reaction with the higher activation energy has the lower rate constant and the slower rate. The larger value of E _a results in a smaller value for $e^{\text{−}{E}_{\text{a}}\text{/}RT},$ reflecting the smaller fraction of molecules with enough energy to react. Alternatively, the reaction with the smaller E _a has a larger fraction of molecules with enough energy to react. This will be reflected as a larger value of $e^{\text{−}{E}_{\text{a}}\text{/}RT},$ a larger rate constant, and a faster rate for the reaction. An increase in temperature has the same effect as a decrease in activation energy. A larger fraction of molecules has the necessary energy to react ( [link] ), as indicated by an increase in the value of $e^{\text{−}{E}_{\text{a}}\text{/}RT}.$ The rate constant is also directly proportional to the frequency factor, A . Hence a change in conditions or reactants that increases the number of collisions with a favorable orientation for reaction results in an increase in A and, consequently, an increase in k .