1. Home
  2. Mechanics
  3. Rotational motion and angular
  4. Rotational kinetic energy: work

9.4 Rotational kinetic energy: work and energy revisited  (Page 5/9)

<< Chapter < Page
  Mechanics     Page 5 / 9
Chapter >> Page >
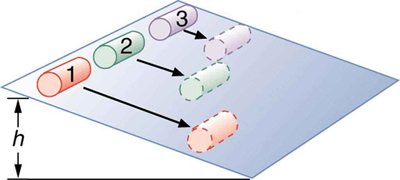
The figure shows a flat surface inclined at a height of h from the surface level, with three cans of soup of different densities numbered as one, two, and three rolling along it.
Three cans of soup with identical masses race down an incline. The first can has a low friction coating and does not roll but just slides down the incline. It wins because it converts its entire PE into translational KE. The second and third cans both roll down the incline without slipping. The second can contains thin soup and comes in second because part of its initial PE goes into rotating the can (but not the thin soup). The third can contains thick soup. It comes in third because the soup rotates along with the can, taking even more of the initial PE for rotational KE, leaving less for translational KE.

Assuming no losses due to friction, there is only one force doing work—gravity. Therefore the total work done is the change in kinetic energy. As the cans start moving, the potential energy is changing into kinetic energy. Conservation of energy gives

PE i = KE f . size 12{"PE" rSub { size 8{i} } ="KE" rSub { size 8{f} } } {}

More specifically,

PE grav = KE trans + KE rot size 12{"PE" rSub { size 8{"grav"} } ="KE" rSub { size 8{"trans"} } +"KE" rSub { size 8{"rot"} } } {}

or

mgh = 1 2 mv 2 + 1 2 Iω 2 . size 12{ ital "mgh"= { {1} over {2} } ital "mv" rSup { size 8{2} } + { {1} over {2} } Iω rSup { size 8{2} } } {}

So, the initial mgh size 12{ ital "mgh"} {} is divided between translational kinetic energy and rotational kinetic energy; and the greater I size 12{I} {} is, the less energy goes into translation. If the can slides down without friction, then ω = 0 size 12{ω=0} {} and all the energy goes into translation; thus, the can goes faster.

Take-home experiment

Locate several cans each containing different types of food. First, predict which can will win the race down an inclined plane and explain why. See if your prediction is correct. You could also do this experiment by collecting several empty cylindrical containers of the same size and filling them with different materials such as wet or dry sand.

Calculating the speed of a cylinder rolling down an incline

Calculate the final speed of a solid cylinder that rolls down a 2.00-m-high incline. The cylinder starts from rest, has a mass of 0.750 kg, and has a radius of 4.00 cm.

Strategy

We can solve for the final velocity using conservation of energy, but we must first express rotational quantities in terms of translational quantities to end up with v as the only unknown.

Solution

Conservation of energy for this situation is written as described above:

mgh = 1 2 mv 2 + 1 2 Iω 2 . size 12{ ital "mgh"= { {1} over {2} } ital "mv" rSup { size 8{2} } + { {1} over {2} } Iω rSup { size 8{2} } } {}

Before we can solve for v size 12{v} {} , we must get an expression for I size 12{I} {} from [link] . Because v size 12{v} {} and ω size 12{ω} {} are related (note here that the cylinder is rolling without slipping), we must also substitute the relationship ω = v / R size 12{ω=v/R} {} into the expression. These substitutions yield

mgh = 1 2 mv 2 + 1 2 1 2 mR 2 v 2 R 2 . size 12{ ital "mgh"= { {1} over {2} } ital "mv" rSup { size 8{2} } + { {1} over {2} } left ( { {1} over {2} } ital "mR" rSup { size 8{2} } right ) left ( { {v rSup { size 8{2} } } over {R rSup { size 8{2} } } } right )} {}

Interestingly, the cylinder’s radius R and mass m cancel, yielding

gh = 1 2 v 2 + 1 4 v 2 = 3 4 v 2 . size 12{ ital "gh"= { {1} over {2} } v rSup { size 8{2} } + { {1} over {4} } v rSup { size 8{2} } = { {3} over {4} } v rSup { size 8{2} } } {}

Solving algebraically, the equation for the final velocity v size 12{v} {} gives

v = 4 gh 3 1 / 2 . size 12{v= left ( { {4 ital "gh"} over {3} } right ) rSup { size 8{1/2} } } {}

Substituting known values into the resulting expression yields

v = 4 9.80 m/s 2 2.00 m 3 1 / 2 = 5.11 m/s . size 12{v= left [ { {4 left (9 "." "80"" m/s" rSup { size 8{2} } right ) left (2 "." "00"" m" right )} over {3} } right ] rSup { size 8{1/2} } =5 "." "11"" m/s"} {}

Discussion

Because m size 12{m} {} and R size 12{R} {} cancel, the result v = 4 3 gh 1 / 2 size 12{v= left ( { {4} over {3} } ital "gh" right ) rSup { size 8{1/2} } } {} is valid for any solid cylinder, implying that all solid cylinders will roll down an incline at the same rate independent of their masses and sizes. (Rolling cylinders down inclines is what Galileo actually did to show that objects fall at the same rate independent of mass.) Note that if the cylinder slid without friction down the incline without rolling, then the entire gravitational potential energy would go into translational kinetic energy. Thus, 1 2 mv 2 = mgh size 12{ \( 1/2 \) ital "mv" rSup { size 8{2} } `= ital "mgh"} {} and v = ( 2 gh ) 1 / 2 size 12{v= \( 2 ital "gh" \) rSup { size 8{1/2} } } {} , which is 22% greater than ( 4 gh / 3 ) 1 / 2 size 12{ \( 4 ital "gh"/3 \) rSup { size 8{1/2} } } {} . That is, the cylinder would go faster at the bottom.
<< Chapter < Page Page > Chapter >>
Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Mechanics. OpenStax CNX. Apr 15, 2013 Download for free at http://legacy.cnx.org/content/col11506/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Mechanics' conversation and receive update notifications?

Ask