| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
So far in this chapter, we have focused on solving word problems, which are similar to many real-world applications of algebra. In the next few sections, we will apply our problem-solving strategies to some common geometry problems.
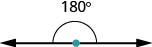
Are you familiar with the phrase ‘do a It means to make a full turn so that you face the opposite direction. It comes from the fact that the measure of an angle that makes a straight line is degrees. See [link] .
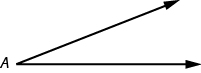
An angle is formed by two rays that share a common endpoint. Each ray is called a side of the angle and the common endpoint is called the vertex . An angle is named by its vertex. In [link] , is the angle with vertex at point The measure of is written
We measure angles in degrees, and use the symbol to represent degrees. We use the abbreviation to for the measure of an angle. So if is we would write
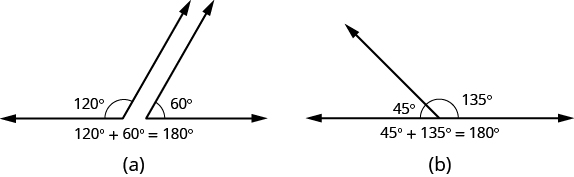
If the sum of the measures of two angles is then they are called supplementary angles . In [link] , each pair of angles is supplementary because their measures add to Each angle is the supplement of the other.
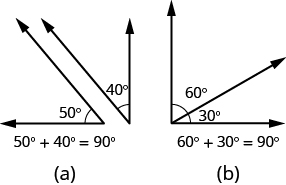
If the sum of the measures of two angles is then the angles are complementary angles . In [link] , each pair of angles is complementary, because their measures add to Each angle is the complement of the other.
If the sum of the measures of two angles is then the angles are supplementary.
If
and
are supplementary, then
If the sum of the measures of two angles is
then the angles are complementary.
If
and
are complementary, then
In this section and the next, you will be introduced to some common geometry formulas. We will adapt our Problem Solving Strategy for Geometry Applications. The geometry formula will name the variables and give us the equation to solve.
In addition, since these applications will all involve geometric shapes, it will be helpful to draw a figure and then label it with the information from the problem. We will include this step in the Problem Solving Strategy for Geometry Applications.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?