| << Chapter < Page | Chapter >> Page > |
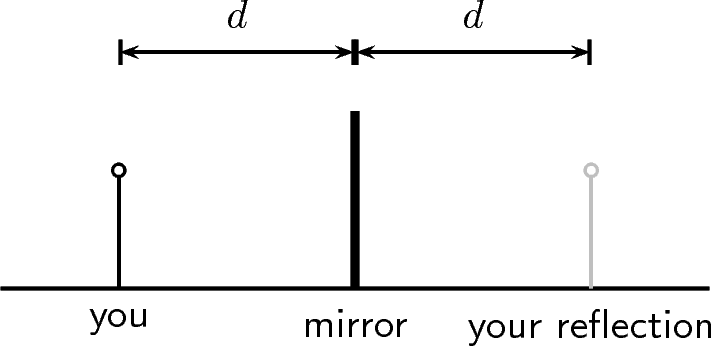
When you stand in front of a mirror your reflection is located the same distance ( ) behind the mirror as you are standing in front of the mirror.
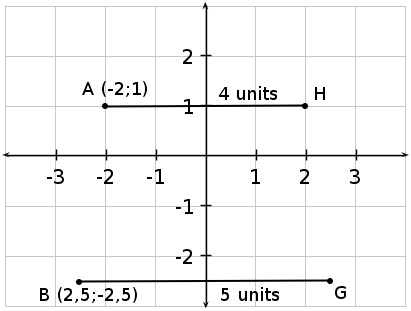
We can apply the same idea to a point that is reflected on the -axis, the -axis and the line .
If a point is reflected on the -axis, then the reflection must be the same distance below the -axis as the point is above the -axis and vice-versa, as though it were a mirror image.
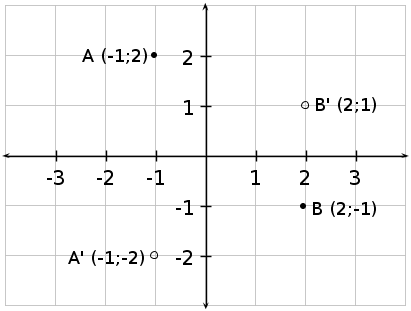
Find the co-ordinates of the reflection of the point P, if P is reflected on the -axis. The co-ordinates of P are (5;10).
We are given the point P with co-ordinates (5;10) and need to find the co-ordinates of the point if it is reflected on the -axis.
The point P is above the -axis, therefore its reflection will be the same distance below the -axis as the point P is above the -axis. Therefore, =-10.
For a reflection on the -axis, the co-ordinate remains unchanged. Therefore, =5.
The co-ordinates of the reflected point are (5;-10).
If a point is reflected on the -axis, then the reflection must be the same distance to the left of the -axis as the point is to the right of the -axis and vice-versa.
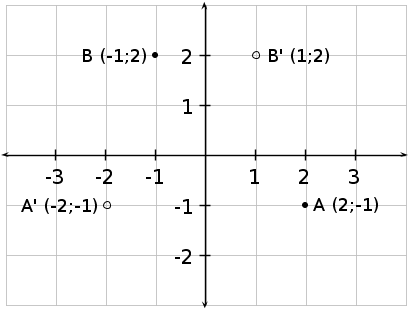
Find the co-ordinates of the reflection of the point Q, if Q is reflected on the -axis. The co-ordinates of Q are (15;5).
We are given the point Q with co-ordinates (15;5) and need to find the co-ordinates of the point if it is reflected on the -axis.
The point Q is to the right of the -axis, therefore its reflection will be the same distance to the left of the -axis as the point Q is to the right of the -axis. Therefore, =-15.
For a reflection on the -axis, the co-ordinate remains unchanged. Therefore, =5.
The co-ordinates of the reflected point are (-15;5).
The final type of reflection you will learn about is the reflection of a point on the line .
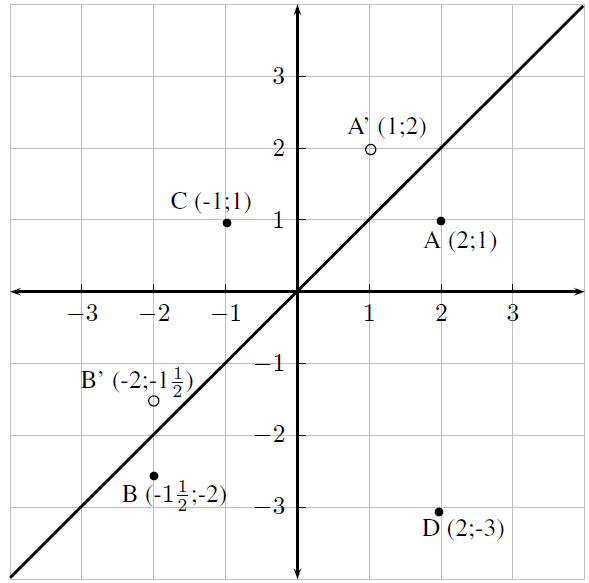
Study the information given and complete the following table:
| Point | Reflection | |
| A | (2;1) | (1;2) |
| B | (- ;-2) | (-2;-1 ) |
| C | (-1;1) | |
| D | (2;-3) |

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 maths [caps]' conversation and receive update notifications?