9.2 Comparing two independent population means with unknown population

1. The two independent samples are simple random samples from two distinct populations.
2. Both populations are normally distributed with the population means and standard deviations unknown unless the sample sizes are greater than 30. In that case, the populations need not be normally distributed.

The comparison of two population means is very common. A difference between the two samples depends on both the means and the standard deviations. Verydifferent means can occur by chance if there is great variation among the individual samples. In order to account for the variation, we take the difference of the samplemeans, $\overline{X_1}$ - $\overline{X_2}$ , and divide by the standard error (shown below) in order to standardize the difference. The result is a t-score test statistic (shown below).

Because we do not know the population standard deviations, we estimate them using the two sample standard deviations from our independent samples. For thehypothesis test, we calculate the estimated standard deviation, or standard error , of the difference in sample means , $\overline{X_1}$ - $\overline{X_2}$ .

The test statistic (t-score) is calculated as follows:

Where:

• $s_1$ and $s_2$ , the sample standard deviations, are estimates of ${\sigma }_1$ and ${\sigma }_2$ , respectively.
• ${\sigma }_1$ and ${\sigma }_2$ are the unknown population standard deviations.
• $\overline{x_1}$ and $\overline{x_2}$ are the sample means. ${\mu }_1$ and ${\mu }_2$ are the population means.

The degrees of freedom (df) is a somewhat complicated calculation. However, a computer or calculator calculates it easily. The dfs are not always a whole number. The test statisticcalculated above is approximated by the student's-t distribution with dfs as follows:

When both sample sizes $n_1$ and $n_2$ are five or larger, the student's-t approximation is very good. Notice that the sample variances ${s_1}^2$ and ${s_2}^2$ are not pooled. (If the question comes up, do not pool the variances.)

Independent groups

The average amount of time boys and girls ages 7 through 11 spend playing sports each day is believed to be the same. Anexperiment is done, data is collected, resulting in the table below. Both populations have a normal distribution.

Is there a difference in the mean amount of time boys and girls ages 7 through 11 play sports each day? Test at the 5% level of significance.

The population standard deviations are not known. Let $g$ be the subscript for girls and $b$ be the subscript for boys. Then, ${\mu }_g$ is the population mean for girls and ${\mu }_b$ is the population mean for boys. This is a test of two independent groups , two population means .

Random variable : $\overline{X_g}-\overline{X_b}$ = difference in the sample mean amount of time girls and boys play sports each day.

$H_o$ : ${\mu }_g={\mu }_b{\mu }_g-{\mu }_b=0$

$H_a$ : ${\mu }_g\ne {\mu }_b{\mu }_g-{\mu }_b\ne 0$

The words "the same" tell you $H_o$ has an "=". Since there are no other words to indicate $H_a$ , then assume "is different." This is a two-tailed test.

Distribution for the test: Use $t_{\mathrm{df}}$ where $\mathrm{df}$ is calculated using the $\mathrm{df}$ formula for independent groups, two population means. Using a calculator, $\mathrm{df}$ is approximately 18.8462. Do not pool the variances.

Calculate the p-value using a student's-t distribution: p-value = 0.0054

Graph:

$s_g=\sqrt{0.75}$

$s_b=1$

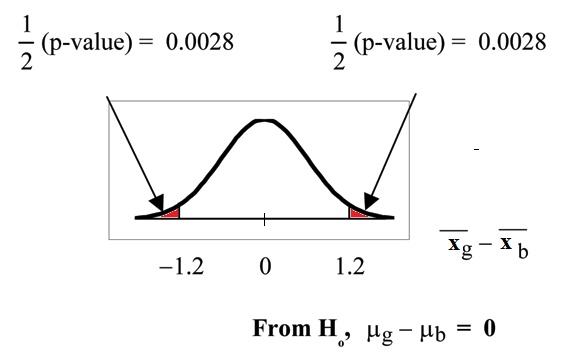
So, $\overline{x_g}-\overline{x_b}=2-3.2=-1.2$

Half the p-value is below -1.2 andhalf is above 1.2.

Make a decision: Since $\alpha >$ p-value, reject $H_o$ .

This means you reject ${\mu }_g={\mu }_b$ . The means are different.

Conclusion: At the 5% level of significance, the sample data show there is sufficient evidence to conclude that the mean number of hours that girls and boys aged 7through 11 play sports per day is different (mean number of hours boys aged 7 through 11 play sports per day is greater than the mean number of hours played by girls OR the mean number of hours girls aged 7 through 11 play sports per day is greater than the mean number of hours played by boys).

TI-83+ and TI-84: Press STAT . Arrow over to TESTS and press 4:2-SampTTest . Arrow over to Stats and press ENTER . Arrow down and enter 2 for the first sample mean, $\sqrt{0.75}$ for Sx1, 9 for n1, 3.2 for the second sample mean, 1 for Sx2, and 16 for n2. Arrow down to μ1: and arrow to does not equal μ2. Press ENTER . Arrow down to Pooled: and No . Press ENTER . Arrow down to Calculate and press ENTER . The p-value is p = 0.0054, the dfs are approximately 18.8462, and the teststatistic is -3.14. Do the procedure again but instead of Calculate do Draw.