9.2 Comparing two independent population means with known population

This is a test of two independent groups, two population means, population standard deviations known.

Random Variable : $\overline{X_1}-\overline{X_2}=$ difference in the mean number of months the competing floor waxes last.

$H_o:{\mu }_1\le {\mu }_2$

$H_a:{\mu }_1>{\mu }_2$

The words "is more effective" says that wax 1 lasts longer than wax 2 , on the average. "Longer" is a $">"$ symbol and goes into $H_a$ . Therefore, this is a right-tailed test.

Distribution for the test: The population standard deviations are known so the distribution is normal. Using the formula above, the distribution is:

$\overline{X_1}-\overline{X_2}~N(0,\sqrt{\frac{{0.33}^2}{20}+\frac{{0.36}^2}{20}})$

Since ${\mu }_1\le {\mu }_2$ then ${\mu }_1-{\mu }_2\le 0$ and the mean for the normal distributionis 0.

Calculate the p-value using the normal distribution: p-value = 0.1799

Graph:

$\overline{x_1}-\overline{x_2}=3-2.9=0.1$

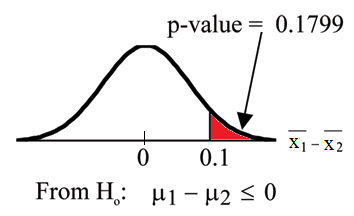
Compare α and the p-value: $\alpha =0.05$ and p-value = 0.1799. Therefore, $\alpha <$ p-value.

Make a decision: Since $\alpha <$ p-value, do not reject $H_o$ .

Conclusion: At the 5% level of significance, from the sample data, there is not sufficient evidence to conclude that the mean time wax 1 lasts is longer (wax 1 is more effective) than the mean time wax 2 lasts.