9.15 Image formation by mirrors  (Page 6/9)

What are the differences between real and virtual images? How can you tell (by looking) whether an image formed by a single lens or mirror is real or virtual?

Can you see a virtual image? Can you photograph one? Can one be projected onto a screen with additional lenses or mirrors? Explain your responses.

Is it necessary to project a real image onto a screen for it to exist?

At what distance is an image always located—at $d_{\text{o}}$ , $d_{\text{i}}$ , or $f$ ?

Under what circumstances will an image be located at the focal point of a lens or mirror?

What is meant by a negative magnification? What is meant by a magnification that is less than 1 in magnitude?

Can a case 1 image be larger than the object even though its magnification is always negative? Explain.

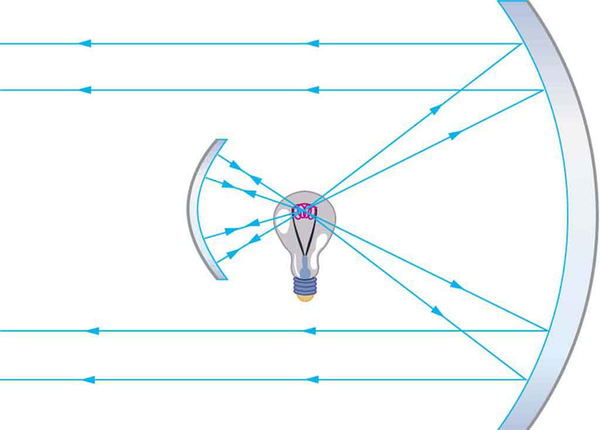
[link] shows a light bulb between two mirrors. One mirror produces a beam of light with parallel rays; the other keeps light from escaping without being put into the beam. Where is the filament of the light in relation to the focal point or radius of curvature of each mirror?

Devise an arrangement of mirrors allowing you to see the back of your head. What is the minimum number of mirrors needed for this task?

If you wish to see your entire body in a flat mirror (from head to toe), how tall should the mirror be? Does its size depend upon your distance away from the mirror? Provide a sketch.

It can be argued that a flat mirror has an infinite focal length. If so, where does it form an image? That is, how are $d_{\text{i}}$ and $d_{\text{o}}$ related?

Why are diverging mirrors often used for rear-view mirrors in vehicles? What is the main disadvantage of using such a mirror compared with a flat one?

What is the focal length of a makeup mirror that has a power of 1.50 D?

Some telephoto cameras use a mirror rather than a lens. What radius of curvature mirror is needed to replace a 800 mm focal length telephoto lens?

(a) Calculate the focal length of the mirror formed by the shiny back of a spoon that has a 3.00 cm radius of curvature. (b) What is its power in diopters?

Find the magnification of the heater element in [link] . Note that its large magnitude helps spread out the reflected energy.

What is the focal length of a makeup mirror that produces a magnification of 1.50 when a person’s face is 12.0 cm away?

A shopper standing 3.00 m from a convex security mirror sees his image with a magnification of 0.250. (a) Where is his image? (b) What is the focal length of the mirror? (c) What is its radius of curvature?

An object 1.50 cm high is held 3.00 cm from a person’s cornea, and its reflected image is measured to be 0.167 cm high. (a) What is the magnification? (b) Where is the image? (c) Find the radius of curvature of the convex mirror formed by the cornea. (Note that this technique is used by optometrists to measure the curvature of the cornea for contact lens fitting. The instrument used is called a keratometer, or curve measurer.)

Ray tracing for a flat mirror shows that the image is located a distance behind the mirror equal to the distance of the object from the mirror. This is stated $d_{\text{i}}={\mathrm{–d}}_{\text{o}}$ , since this is a negative image distance (it is a virtual image). (a) What is the focal length of a flat mirror? (b) What is its power?

Show that for a flat mirror $h_{\text{i}}=h_{\text{o}}$ , knowing that the image is a distance behind the mirror equal in magnitude to the distance of the object from the mirror.

Use the law of reflection to prove that the focal length of a mirror is half its radius of curvature. That is, prove that $f=R/2$ . Note this is true for a spherical mirror only if its diameter is small compared with its radius of curvature.

Referring to the electric room heater considered in the first example in this section, calculate the intensity of IR radiation in ${\text{W/m}}^2$ projected by the concave mirror on a person 3.00 m away. Assume that the heating element radiates 1500 W and has an area of $\text{100}{\text{cm}}^2$ , and that half of the radiated power is reflected and focused by the mirror.

Consider a 250-W heat lamp fixed to the ceiling in a bathroom. If the filament in one light burns out then the remaining three still work. Construct a problem in which you determine the resistance of each filament in order to obtain a certain intensity projected on the bathroom floor. The ceiling is 3.0 m high. The problem will need to involve concave mirrors behind the filaments. Your instructor may wish to guide you on the level of complexity to consider in the electrical components.