| << Chapter < Page | Chapter >> Page > |
The sum of four times a number and two is Find the number.
3
The sum of three times a number and seven is Find the number.
6
Some number word problems ask you to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. We will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
One number is five more than another. The sum of the numbers is twenty-one. Find the numbers.
| Step 1. Read the problem. | ||
| Step 2. Identify what you are looking for. | You are looking for two numbers. | |
| Step 3.
Name.
Choose a variable to represent the first number. What do you know about the second number? |
Let One number is five more than another. | |
| Step 4.
Translate.
Restate the problem as one sentence with all the important information. Translate into an equation. Substitute the variable expressions. |
The sum of the numbers is 21. The sum of the 1st number and the 2nd number is 21. | |
| Step 5. Solve the equation. |
| |
| Combine like terms. |
| |
| Subtract five from both sides and simplify. |
| |
| Divide by two and simplify. |
| |
| Find the second number too. |
| |
| Substitute n = 8 |
| |
|
| ||
| Step 6.
Check:
Do these numbers check in the problem? Is one number 5 more than the other? Is thirteen, 5 more than 8? Yes. Is the sum of the two numbers 21? |
|
|
| Step 7. Answer the question. | The numbers are 8 and 13. |
One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.
9, 15
The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.
27, 31
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
| Step 1. Read the problem. | ||
| Step 2. Identify what you are looking for. | two numbers | |
| Step 3.
Name. Choose a variable.
What do you know about the second number? Translate. |
Let n = 1 st number One number is 4 less than the other. n - 4 = 2 nd number | |
| Step 4.
Translate.
Write as one sentence. Translate into an equation. Substitute the variable expressions. |
The sum of two numbers is negative fourteen. 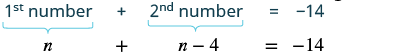 | |
| Step 5. Solve the equation. |
| |
| Combine like terms. |
| |
| Add 4 to each side and simplify. |
| |
| Simplify. |
| |
|
| ||
|
| ||
|
| ||
| Step 6.
Check:
Is −9 four less than −5? Is their sum −14? |
|
|
| Step 7. Answer the question. | The numbers are −5 and −9. |
The sum of two numbers is negative twenty-three. One number is less than the other. Find the numbers.
−8, −15
The sum of two numbers is negative eighteen. One number is more than the other. Find the numbers.
−29, 11
One number is ten more than twice another. Their sum is one. Find the numbers.
| Step 1. Read the problem. | ||
| Step 2. Identify what you are looking for. | two numbers | |
| Step 3.
Name. Choose a variable.
One number is ten more than twice another. |
Let
x = 1
st number
2 x + 10 = 2 nd number | |
| Step 4. Translate. Restate as one sentence. | Their sum is one. | |
| Translate into an equation |
 | |
| Step 5. Solve the equation. |
| |
| Combine like terms. |
| |
| Subtract 10 from each side. |
| |
| Divide each side by 3 to get the first number. |
| |
| Substitute to get the second number. |
| |
|
| ||
|
| ||
| Step 6.
Check.
Is 4 ten more than twice −3? Is their sum 1? |
|
|
| Step 7. Answer the question. | The numbers are −3 and 4. |

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?