8.6 Forces and torques in muscles and joints  (Page 4/6)

Strategy

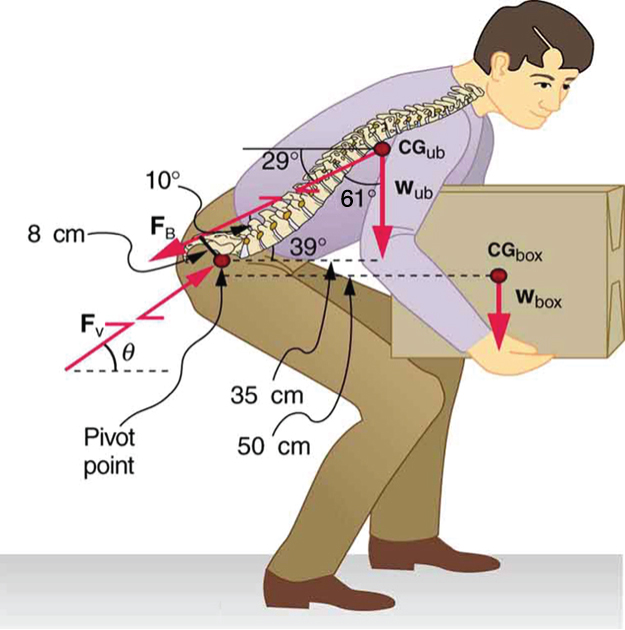
By now, we sense that the second condition for equilibrium is a good place to start, and inspection of the known values confirms that it can be used to solve for $F_{\text{B}}–$ if the pivot is chosen to be at the hips. The torques created by ${\mathbf{\text{w}}}_{\text{ub}}$ and ${\mathbf{\text{w}}}_{\text{box}}–$ are clockwise, while that created by ${\mathbf{\text{F}}}_{\text{B}}–$ is counterclockwise.

Solution for (a)

Using the perpendicular lever arms given in the figure, the second condition for equilibrium $\left(\text{net}\tau =\text{0}\right)$ becomes

Solving for $F_{\text{B}}$ yields

The ratio of the force the back muscles exert to the weight of the upper body plus its load is

This force is considerably larger than it would be if the load were not present.

Solution for (b)

More important in terms of its damage potential is the force on the vertebrae ${\mathbf{\text{F}}}_{\text{V}}$ . The first condition for equilibrium ( $\text{net}\mathbf{\text{F}}=0$ ) can be used to find its magnitude and direction. Using $y$ for vertical and $x$ for horizontal, the condition for the net external forces along those axes to be zero

Starting with the vertical ( $y$ ) components, this yields

Thus,

yielding

Similarly, for the horizontal ( $x$ ) components,

yielding

The magnitude of ${\mathbf{\text{F}}}_{\text{V}}$ is given by the Pythagorean theorem:

The direction of ${\mathbf{\text{F}}}_{\text{V}}$ is

Note that the ratio of $F_{\text{V}}$ to the weight supported is

Discussion

This force is about 5.6 times greater than it would be if the person were standing erect. The trouble with the back is not so much that the forces are large—because similar forces are created in our hips, knees, and ankles—but that our spines are relatively weak. Proper lifting, performed with the back erect and using the legs to raise the body and load, creates much smaller forces in the back—in this case, about 5.6 times smaller.

What are the benefits of having most skeletal muscles attached so close to joints? One advantage is speed because small muscle contractions can produce large movements of limbs in a short period of time. Other advantages are flexibility and agility, made possible by the large numbers of joints and the ranges over which they function. For example, it is difficult to imagine a system with biceps muscles attached at the wrist that would be capable of the broad range of movement we vertebrates possess.

There are some interesting complexities in real systems of muscles, bones, and joints. For instance, the pivot point in many joints changes location as the joint is flexed, so that the perpendicular lever arms and the mechanical advantage of the system change, too. Thus the force the biceps muscle must exert to hold up a book varies as the forearm is flexed. Similar mechanisms operate in the legs, which explain, for example, why there is less leg strain when a bicycle seat is set at the proper height. The methods employed in this section give a reasonable description of real systems provided enough is known about the dimensions of the system. There are many other interesting examples of force and torque in the body—a few of these are the subject of end-of-chapter problems.