8.6 Forces and torques in muscles and joints  (Page 14/6)

Muscles exert bigger forces than you might think

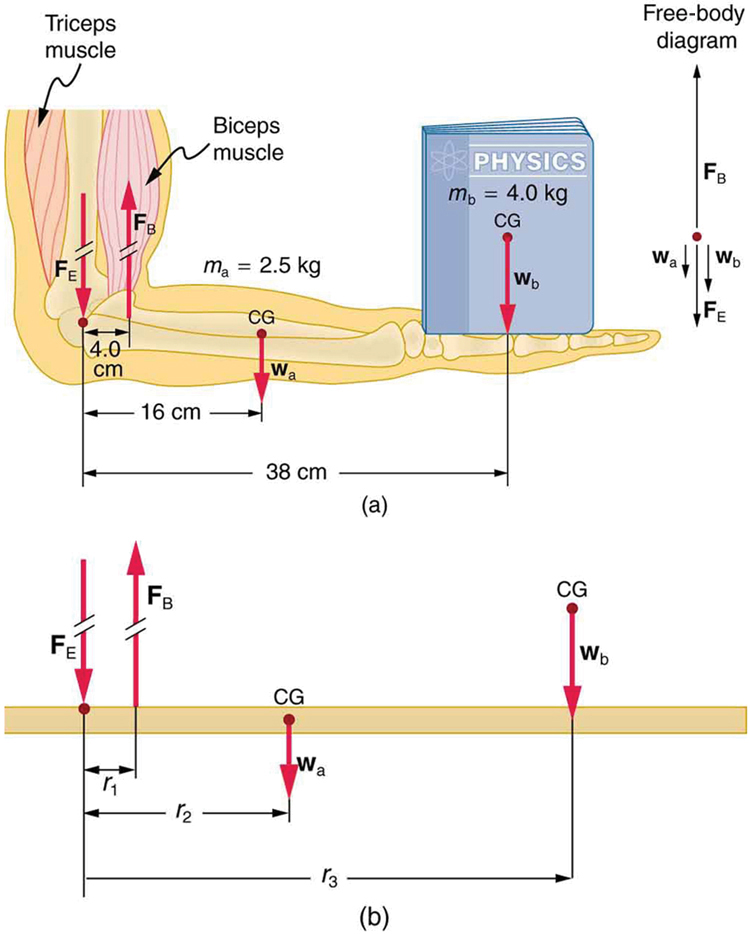
Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in [link] , and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.

Strategy

There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is $F_{\text{B}}$ ; that of the elbow joint is $F_{\text{E}}$ ; that of the weights of the forearm is $w_{\text{a}}$ , and its load is $w_{\text{b}}$ . Two of these are unknown ( $F_{\text{B}}$ and $F_{\text{E}}$ ), so that the first condition for equilibrium cannot by itself yield $F_{\text{B}}$ . But if we use the second condition and choose the pivot to be at the elbow, then the torque due to $F_{\text{E}}$ is zero, and the only unknown becomes $F_{\text{B}}$ .

Solution

The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium $\left(\text{net}\tau =\text{0}\right)$ becomes

Note that $\text{sin}\theta =1$ for all forces, since $\theta =\text{90º}$ for all forces. This equation can easily be solved for $F_{\text{B}}$ in terms of known quantities, yielding

Entering the known values gives

which yields

Now, the combined weight of the arm and its load is $\left(\text{6.50 kg}\right)\left(\text{9.80}{\text{m/s}}^2\right)=\text{63.7 N}$ , so that the ratio of the force exerted by the biceps to the total weight is

Discussion

This means that the biceps muscle is exerting a force 7.38 times the weight supported.