1. Home
  2. Physics of the world around us
  3. Fluids and bouyant force
  4. Variation of pressure with depth

8.4 Variation of pressure with depth in a fluid  (Page 2/4)

<< Chapter < Page
  Physics of the world around us     Page 2 / 4
Chapter >> Page >
A two-dimensional view of a dam with dimensions L and h is shown. Force F at h is shown by a horizontal arrow. The force F exerted by water on the dam is F equals average pressure p bar into area A and pressure in turn is average height h bar into density rho into acceleration due to gravity g.
The dam must withstand the force exerted against it by the water it retains. This force is small compared with the weight of the water behind the dam.

Atmospheric pressure is another example of pressure due to the weight of a fluid, in this case due to the weight of air above a given height. The atmospheric pressure at the Earth’s surface varies a little due to the large-scale flow of the atmosphere induced by the Earth’s rotation (this creates weather “highs” and “lows”). However, the average pressure at sea level is given by the standard atmospheric pressure P atm size 12{P rSub { size 8{"atm"} } } {} , measured to be

1 atmosphere (atm) = P atm = 1.01 × 10 5 N/m 2 = 101 kPa . size 12{1`"atmosphere"` \( "atm" \) =P rSub { size 8{"atm"} } =1 "." "01" times "10" rSup { size 8{5} } `"N/m" rSup { size 8{2} } ="101"`"kPa"} {}

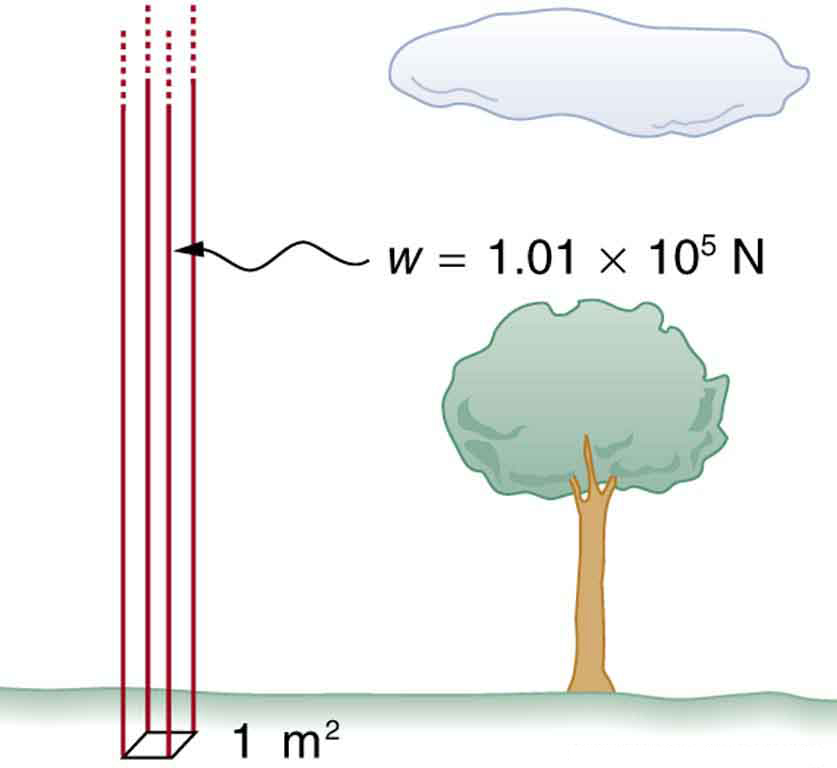
This relationship means that, on average, at sea level, a column of air above 1.00 m 2 of the Earth’s surface has a weight of 1.01 × 10 5 N size 12{1 "." "01" times "10" rSup { size 8{5} } `N} {} , equivalent to 1 atm . (See [link] .)

Figure shows a column of air exerting a weight of one point zero one times ten to the power five newtons on a rectangular patch of ground of one square meter cross section.
Atmospheric pressure at sea level averages 1 . 01 × 10 5 Pa size 12{1 "." "01" times "10" rSup { size 8{5} } `"Pa"} {} (equivalent to 1 atm), since the column of air over this 1 m 2 size 12{1`m rSup { size 8{2} } } {} , extending to the top of the atmosphere, weighs 1 . 01 × 10 5 N size 12{1 "." "01" times "10" rSup { size 8{5} } " N"} {} .

Calculating average density: how dense is the air?

Calculate the average density of the atmosphere, given that it extends to an altitude of 120 km. Compare this density with that of air listed in [link] .

Strategy

If we solve P = hρg size 12{P=hρg} {} for density, we see that

ρ ¯ = P hg . size 12{ { bar {ρ}}= { {P} over { ital "hg"} } } {}

We then take P size 12{P} {} to be atmospheric pressure, h size 12{h} {} is given, and g size 12{g} {} is known, and so we can use this to calculate ρ ¯ size 12{ { bar {ρ}}} {} .

Solution

Entering known values into the expression for ρ ¯ size 12{ { bar {ρ}}} {} yields

ρ ¯ = 1 . 01 × 10 5 N/m 2 ( 120 × 10 3 m ) ( 9 . 80 m/s 2 ) = 8 . 59 × 10 − 2 kg/m 3 . size 12{ { bar {ρ}}= { {1 "." "01" times "10" rSup { size 8{5} } `"N/m" rSup { size 8{2} } } over { \( "120" times "10" rSup { size 8{3} } `m \) \( 9 "." "80"`"m/s" rSup { size 8{2} } \) } } =8 "." "59" times "10" rSup { size 8{ - 2} } `"kg/m" rSup { size 8{3} } } {}

Discussion

This result is the average density of air between the Earth’s surface and the top of the Earth’s atmosphere, which essentially ends at 120 km. The density of air at sea level is given in [link] as 1 . 29 kg/m 3 size 12{1 "." "29"`"kg/m" rSup { size 8{3} } } {} —about 15 times its average value. Because air is so compressible, its density has its highest value near the Earth’s surface and declines rapidly with altitude.

Calculating depth below the surface of water: what depth of water creates the same pressure as the entire atmosphere?

Calculate the depth below the surface of water at which the pressure due to the weight of the water equals 1.00 atm.

Strategy

We begin by solving the equation P = hρg size 12{P=hρg} {} for depth h size 12{h} {} :

h = P ρg . size 12{h= { {P} over {ρg} } } {}

Then we take P size 12{P} {} to be 1.00 atm and ρ size 12{ρ} {} to be the density of the water that creates the pressure.

Solution

Entering the known values into the expression for h size 12{h} {} gives

h = 1 . 01 × 10 5 N/m 2 ( 1 . 00 × 10 3 kg/m 3 ) ( 9 . 80 m/s 2 ) = 10 . 3 m . size 12{h= { {1 "." "01" times "10" rSup { size 8{5} } `"N/m" rSup { size 8{2} } } over { \( 1 "." "00" times "10" rSup { size 8{3} } `"kg/m" rSup { size 8{3} } \) \( 9 "." "80"`"m/s" rSup { size 8{2} } \) } } ="10" "." 3`m} {}

Discussion

Just 10.3 m of water creates the same pressure as 120 km of air. Since water is nearly incompressible, we can neglect any change in its density over this depth.

What do you suppose is the total pressure at a depth of 10.3 m in a swimming pool? Does the atmospheric pressure on the water’s surface affect the pressure below? The answer is yes. This seems only logical, since both the water’s weight and the atmosphere’s weight must be supported. So the total pressure at a depth of 10.3 m is 2 atm—half from the water above and half from the air above. We shall see in Pascal’s Principle that fluid pressures always add in this way.

Section summary

  • Pressure is the weight of the fluid mg size 12{ ital "mg"} {} divided by the area A size 12{A} {} supporting it (the area of the bottom of the container):
    P = mg A . size 12{P= { { ital "mg"} over {A} } } {}
  • Pressure due to the weight of a liquid is given by
    P = hρg , size 12{P=hρg} {}

    where P size 12{P} {} is the pressure, h size 12{h} {} is the height of the liquid, ρ size 12{ρ} {} is the density of the liquid, and g size 12{g} {} is the acceleration due to gravity.
<< Chapter < Page Page > Chapter >>
Practice Key Terms 1

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Physics of the world around us. OpenStax CNX. May 21, 2015 Download for free at http://legacy.cnx.org/content/col11797/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Physics of the world around us' conversation and receive update notifications?

Ask